Rauman 3: Übung C (Optional)

Veröffentlichungsdatum

4. Dezember 2023

In dieser optionalen Übung wollen wir die G-Function für Luftqualitäts-Messstellen und Rotmilan Bewegungen berechnen und vergleichen.

Aufgabe 1

library("sf")
library("dplyr")
library("ggplot2")

rotmilan <- read_sf("datasets/rauman/rotmilan.gpkg")

schweiz <- read_sf("datasets/rauman/schweiz.gpkg")

luftqualitaet <- read_sf("datasets/rauman/luftqualitaet.gpkg")

ggplot(rotmilan) +
  geom_sf(data = schweiz) +
  geom_sf(aes(colour = timestamp), alpha = 0.2) +
  scale_color_datetime(low = "blue", high = "red")

Abbildung 61.1: Eine solche Visualisierung zeigt dir beispielsweise die räumliche Ausdehnung der Datenpunkte

Aufgabe 2

Als erstes berechnen wir die G-Function für die Rotmilanpositionen:

Schritt 1

Mit st_distance() können Distanzen zwischen zwei sf Datensätze berechnet werden. Wird nur ein Datensatz angegeben, wird eine Kreuzmatrix erstellt wo die Distanzen zwischen allen Features zu allen anderen Features dargestellt werden. Wir nützen diese Funktion zur Berechnung der nächsten Nachbarn.

Code

rotmilan_distanzmatrix <- st_distance(rotmilan)

nrow(rotmilan_distanzmatrix)
## [1] 2305
ncol(rotmilan_distanzmatrix)
## [1] 2305
# zeige die ersten 6 Zeilen und Spalten der Matrix
# jeder Wert ist 2x vorhanden (vergleiche Wert [2,1] mit [1,2])
# die Diagonale ist die Distanz zu sich selber (gleich 0)
rotmilan_distanzmatrix[1:6, 1:6]
## Units: [m]
##          1         2         3        4        5        6
## 1     0.00 14362.044 20272.492 35596.07 52519.10 64156.67
## 2 14362.04     0.000  8149.486 29752.74 44809.10 53775.25
## 3 20272.49  8149.486     0.000 22580.04 36848.93 45662.55
## 4 35596.07 29752.737 22580.037     0.00 17223.26 31439.57
## 5 52519.10 44809.096 36848.926 17223.26     0.00 16499.19
## 6 64156.67 53775.250 45662.554 31439.57 16499.19     0.00

Schritt 2

Nun wollen wir wissen, wie gross die kürzeste Distanz von jedem Punkt zu seinem nächsten Nachbarn beträgt, also die kürzeste Distanz pro Zeile. Bevor wir diese ermitteln müssen wir die diagonalen Werte noch entfernen, denn diese stellen ja jeweils die Distanz zu sich selber dar und sind immer 0. Danach kann mit apply() eine Funktion (FUN = min) über die Zeilen (MARGIN = 1) einer Matrix (X = rotmilan_distanzmatrix) gerechnet werden. Zusätzlich müssen wir noch na.rm = TRUE setzen, damit NA Werte von der Berechnung ausgeschlossen werden. Das Resultat ist ein Vektor mit gleich vielen Werten wie Zeilen in der Matrix.

Code

diag(rotmilan_distanzmatrix) <- NA # entfernt alle diagonalen Werte

rotmilan_distanzmatrix[1:6, 1:6]
## Units: [m]
##          1         2         3        4        5        6
## 1       NA 14362.044 20272.492 35596.07 52519.10 64156.67
## 2 14362.04        NA  8149.486 29752.74 44809.10 53775.25
## 3 20272.49  8149.486        NA 22580.04 36848.93 45662.55
## 4 35596.07 29752.737 22580.037       NA 17223.26 31439.57
## 5 52519.10 44809.096 36848.926 17223.26       NA 16499.19
## 6 64156.67 53775.250 45662.554 31439.57 16499.19       NA

rotmilan_mindist <- apply(rotmilan_distanzmatrix, 1, min, na.rm = TRUE)

Schritt 3

Nun müssen wir die Distanzen nach ihrer Grösse sortieren

Code

rotmilan_mindist <- sort(rotmilan_mindist)

Schritt 4

Jetzt berechnen wir die kummulierte Häufigkeit von jeder Distanz berechnen. Die kummulierte Häufikgeit vom ersten Wert ist 1 (der Index des ersten Wertes) dividiert durch die Anzahl Werte insgesamt. Mit seq_along erhalten wir die Indizes aller Werte, mit lenth die Anzahl Werte insgesamt.

Code

kumm_haeufgikeit <- seq_along(rotmilan_mindist) / length(rotmilan_mindist)

Schritt 5

Nun wollen wir die kumulierte Häufigkeit der Werte in einer Verteilungsfunktion (engl: Empirical Cumulative Distribution Function, ECDF) darstellen. Dafür müssen wir die beiden Vektoren zuerst noch in einen Dataframe packen, damit ggplot damit klar kommt.

Code

rotmilan_mindist_df <- data.frame(
  distanzen = rotmilan_mindist,
  kumm_haeufgikeit = kumm_haeufgikeit
)

p <- ggplot() +
  geom_line(data = rotmilan_mindist_df, aes(distanzen, kumm_haeufgikeit)) +
  labs(x = "Distanz (Meter)", y = "Häufigkeit (kummuliert)")
p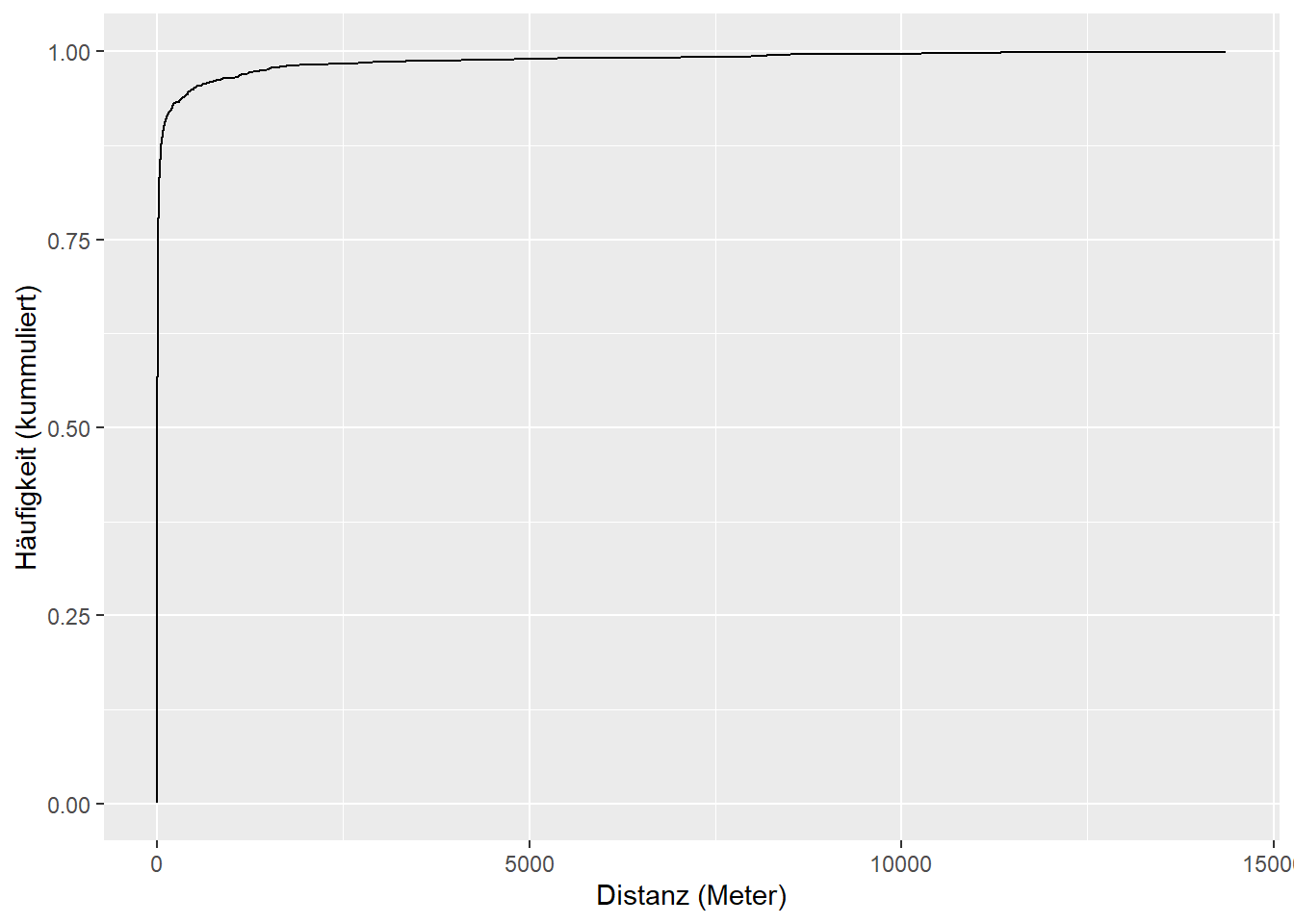

Lesehilfe:

Code

prob <- 0.95
res <- quantile(ecdf(rotmilan_mindist_df$distanzen), prob)
res2 <- quantile(ecdf(rotmilan_mindist_df$distanzen), 0.99)
xlim <- c(5000, NA)
ylim <- c(.5, .75)
p +
  geom_segment(aes(x = res, xend = res, y = -Inf, yend = prob), colour = "lightblue") +
  geom_segment(aes(x = -Inf, xend = res, y = prob, yend = prob), colour = "lightblue") +
  geom_point(aes(x = res, y = prob), size = 3, colour = "lightblue") +
  ggrepel::geom_label_repel(aes(x = 0, y = prob, label = paste0(prob * 100, "% der Werte...")),
    xlim = xlim, ylim = ylim, hjust = 0, min.segment.length = 0, fill = "lightblue"
  ) +
  ggrepel::geom_label_repel(aes(x = res, y = 0, label = paste0("... sind kleiner als ", round(res, 0), "m")),
    xlim = xlim, ylim = ylim, hjust = 0, vjust = 1, fill = "lightblue", min.segment.length = 0, inherit.aes = FALSE
  ) +
  scale_y_continuous(breaks = c(0, .25, .5, .75, prob, 1))

Aufgabe 3

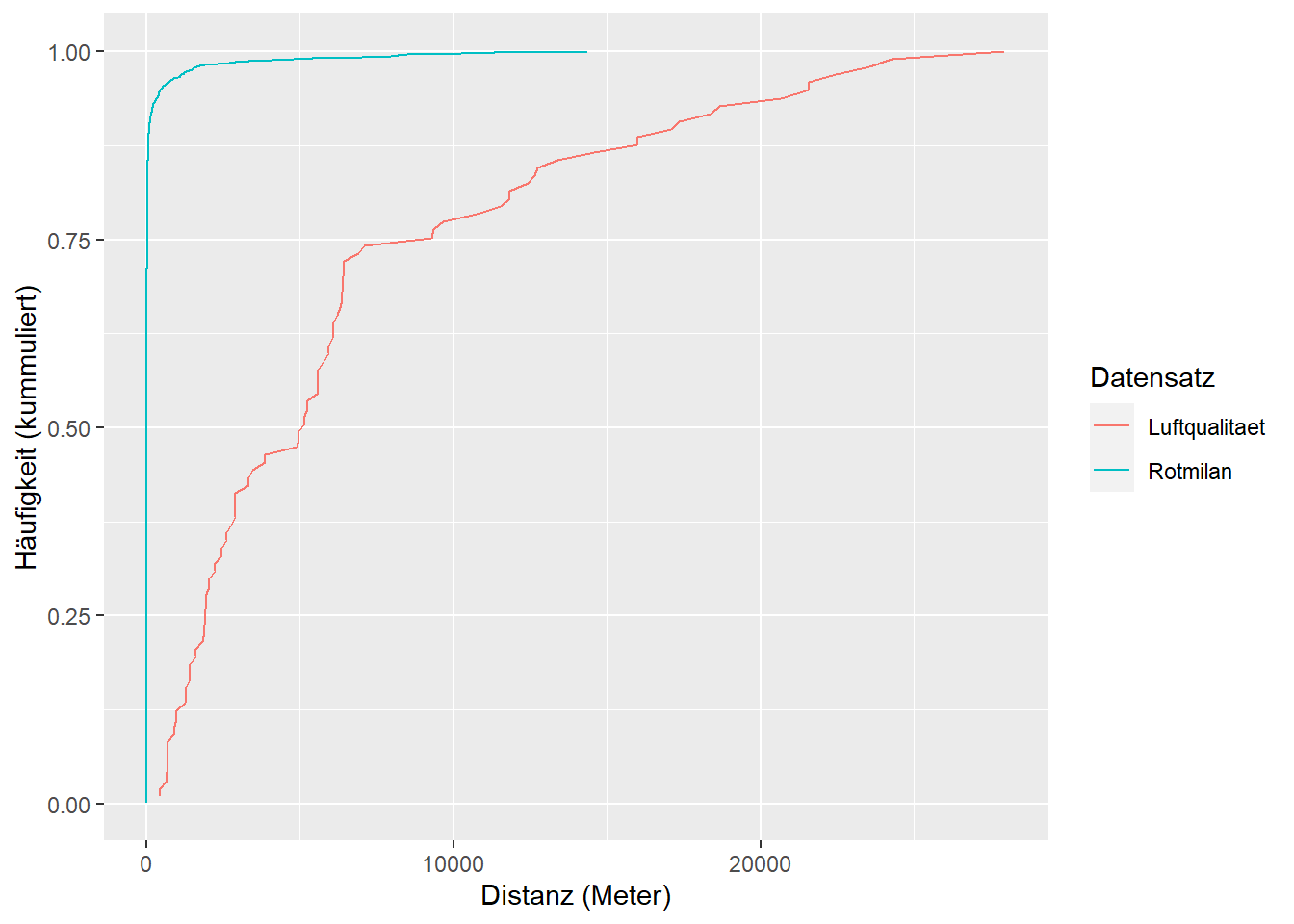
Führe nun die gleichen Schritte mit luftqualitaet durch und vergleiche die ECDF-Plots.

Code

luftqualitaet_distanzmatrix <- st_distance(luftqualitaet)

diag(luftqualitaet_distanzmatrix) <- NA

luftqualitaet_mindist <- apply(luftqualitaet_distanzmatrix, 1, min, na.rm = TRUE)

luftqualitaet_mindist <- sort(luftqualitaet_mindist)

kumm_haeufgikeit_luftquali <- seq_along(luftqualitaet_mindist) / length(luftqualitaet_mindist)

luftqualitaet_mindist_df <- data.frame(
  distanzen = luftqualitaet_mindist,
  kumm_haeufgikeit = kumm_haeufgikeit_luftquali
)

luftqualitaet_mindist_df$data <- "Luftqualitaet"
rotmilan_mindist_df$data <- "Rotmilan"

mindist_df <- rbind(luftqualitaet_mindist_df, rotmilan_mindist_df)

ggplot(mindist_df, ) +
  geom_line(aes(distanzen, kumm_haeufgikeit, colour = data)) +
  labs(x = "Distanz (Meter)", y = "Häufigkeit (kummuliert)", colour = "Datensatz")