library("terra")Rauman 2: Übung B
In der letzten Übung habt ihr nun eine erste Erfahrung mit Raster Daten gemacht. Dabei haben wir zuerst einen Vektordatensatz rasterisiert. Häufig arbeiten wir aber mit Geodaten, die bereits im Rasterformat erfast werden.
Aufgabe 1
In dieser Übung werden wir weiter mit terra arbeiten, um zu zeigen, wie wir einen Rasterdatensatz importieren, visualisieren und weiter verarbeiten können. In euren Daten findet ihr einen Datensatz namens dhm250m.tif, der das “Digitale Höhenmodell” (DHM) des Kantons Schwyz darstellt. Führen Sie den angegebenen Code aus.
Importieren Sie Ihr Raster mit der Funktion rast
dhm_schwyz <- rast("datasets/rauman/dhm250m.tif")Sie erhalten einige wichtige Metadaten über den Rasterdatensatz, wenn Sie den Variablennamen in die Konsole eingeben.
dhm_schwyz
## class : SpatRaster
## dimensions : 150, 186, 1 (nrow, ncol, nlyr)
## resolution : 250, 250 (x, y)
## extent : 2672175, 2718675, 1193658, 1231158 (xmin, xmax, ymin, ymax)
## coord. ref. : CH1903+ / LV95 (EPSG:2056)
## source : dhm250m.tif
## name : dhm250m
## min value : 389.1618
## max value : 2850.0203Um einen schnellen Überblick eines Rasterdatensatz zu erhalten, können wir einfach die plot() Funktion verwenden.
plot(dhm_schwyz)
Leider ist das Verwenden von Rastern in ggplot nicht sehr einfach. Da ggplot ein universelles Plot-Framework ist, stossen wir schnell an die Grenzen des Möglichen, wenn wir etwas so Spezielles wie Karten erstellen. Mit plot können wir zwar sehr schnell plotten, aber auch hier stossen wir schnell an Grenzen.
Aus diesem Grund werden wir ein neues Plot-Framework einführen, das auf Karten spezialisiert ist und in einem sehr ähnlichen Design wie ggplot gebaut wurde: tmap. Laden Sie dieses Paket jetzt in Ihre Session:
library("tmap")Genau wie ggplot basiert tmap auf der Idee von “Ebenen”, die durch ein + verbunden sind. Jede Ebene hat zwei Komponenten:
- eine Datensatzkomponente, die immer
tm_shape(dataset)ist (ersetzen Siedatasetdurch Ihre Variable) - eine Geometriekomponente, die beschreibt, wie das vorangegangene
tm_shape()visualisiert werden soll. Dies kanntm_dots()für Punkte,tm_polygons()für Polygone,tm_lines()für Linien usw. sein. Für Einzelbandraster (was beidhm_schwyzder Fall ist) ist estm_raster()
Code
tm_shape(dhm_schwyz) +
tm_raster()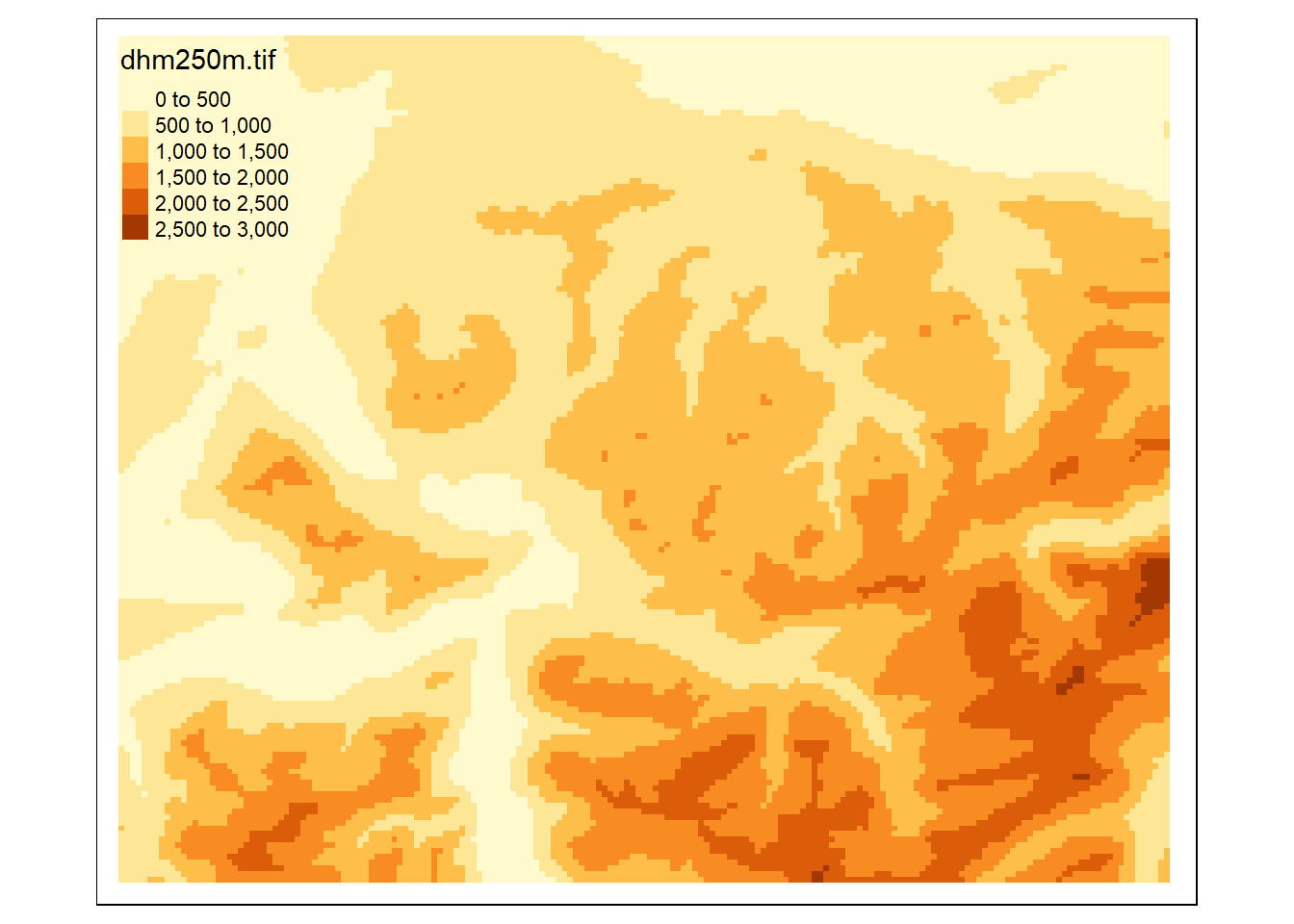
Beachten Sie, dass tm_shape() und tm_raster() (in diesem Fall) zusammengehören. Das eine kann nicht ohne das andere leben.
Wenn Sie die Hilfe von ?tm_raster konsultieren, werden Sie eine Vielzahl von Optionen sehen, mit denen Sie die Visualisierung Ihrer Daten verändern können. Zum Beispiel ist der Standardstil von tm_raster() die Erstellung von “Bins” mit einer diskreten Farbskala. Wir können dies mit style = "cont" ausser Kraft setzen.
Code
tm_shape(dhm_schwyz) +
tm_raster(style = "cont")
Das sieht schon ziemlich toll aus, aber vielleicht wollen wir die Standard-Farbpalette ändern. Glücklicherweise ist das in tmap viel einfacher als in ggplot2. Um sich die verfügbaren Paletten anzusehen, geben Sie tmaptools::palette_explorer() oder RColorBrewer::display.brewer.all() in der Konsole ein (für Ersteres müssen Sie möglicherweise zusätzliche Pakete installieren, z.B. shinyjs).
Code
tm_shape(dhm_schwyz) +
tm_raster(style = "cont", palette = "Spectral")
Eine grosse Stärke von tmap ist die Tatsache, das mit dem gleichen Befehl sowohl statische wie auch interative Plots erstellt werden können. Dafür muss der Modus von statisch auf interaktiv gewechselt werden.
Code
tmap_mode("view") # wechselt auf interakive Plots
tm_shape(dhm_schwyz) +
tm_raster(style = "cont", palette = "Spectral")Code
tmap_mode("plot") # wechselt zurück auf statische PlotsAufgabe 2
Mit terra können wir eine Vielzahl von Rasteroperationen über unser Höhenmodell laufen lassen. Eine klassische Rasteroperation ist zum Beispiel das Berechnen der Hangneigung (“slope”) oder dessen Orientierung (“aspect”). Nutzen Sie die Funktion terrain() aus terra um die Hangneigung und Orientierung zu berechnen. Visualisieren Sie die Resultate.
Code
terrain(dhm_schwyz, "slope") |>
plot()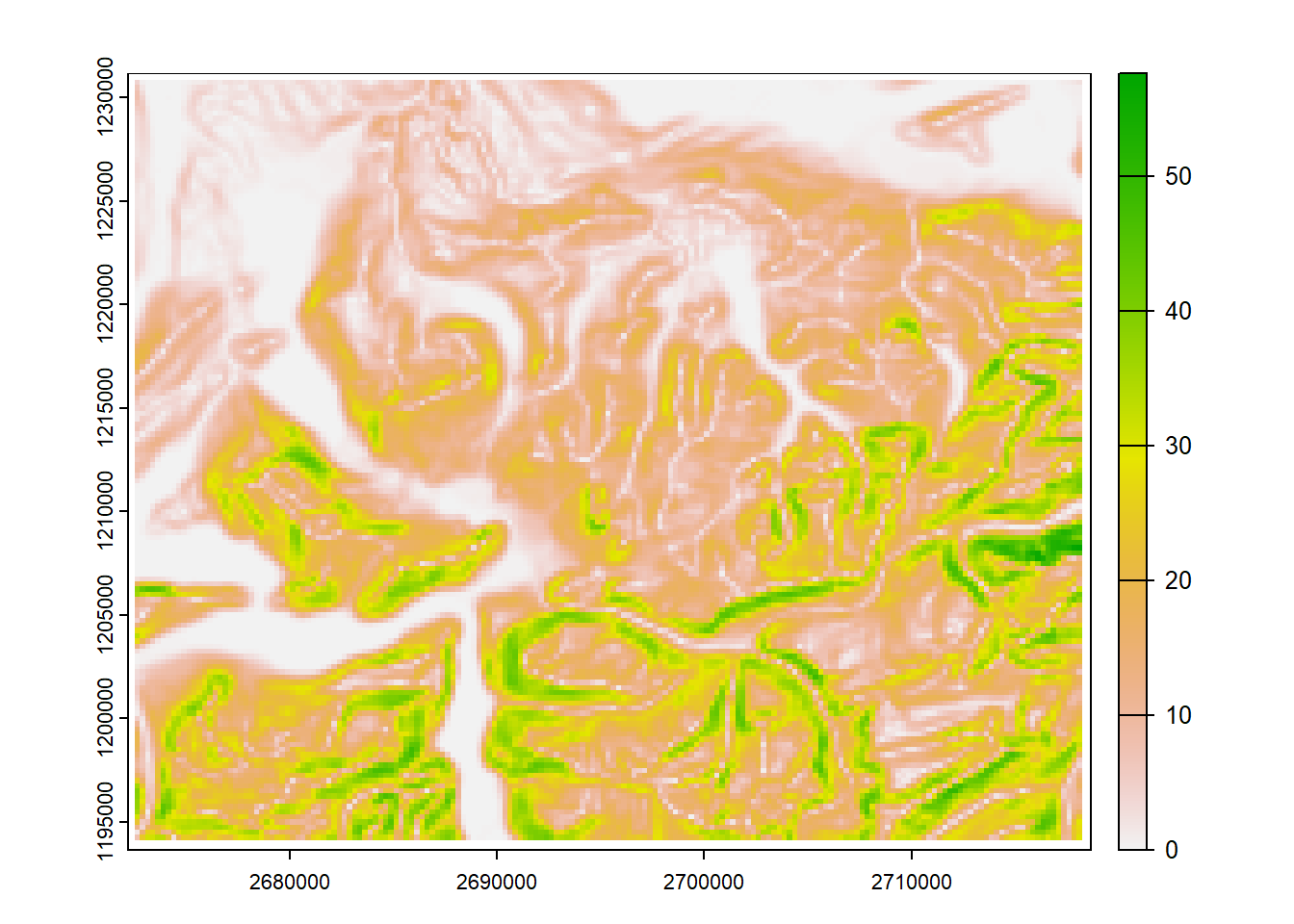
Code
schwyz_aspect <- terrain(dhm_schwyz, "aspect")
plot(schwyz_aspect)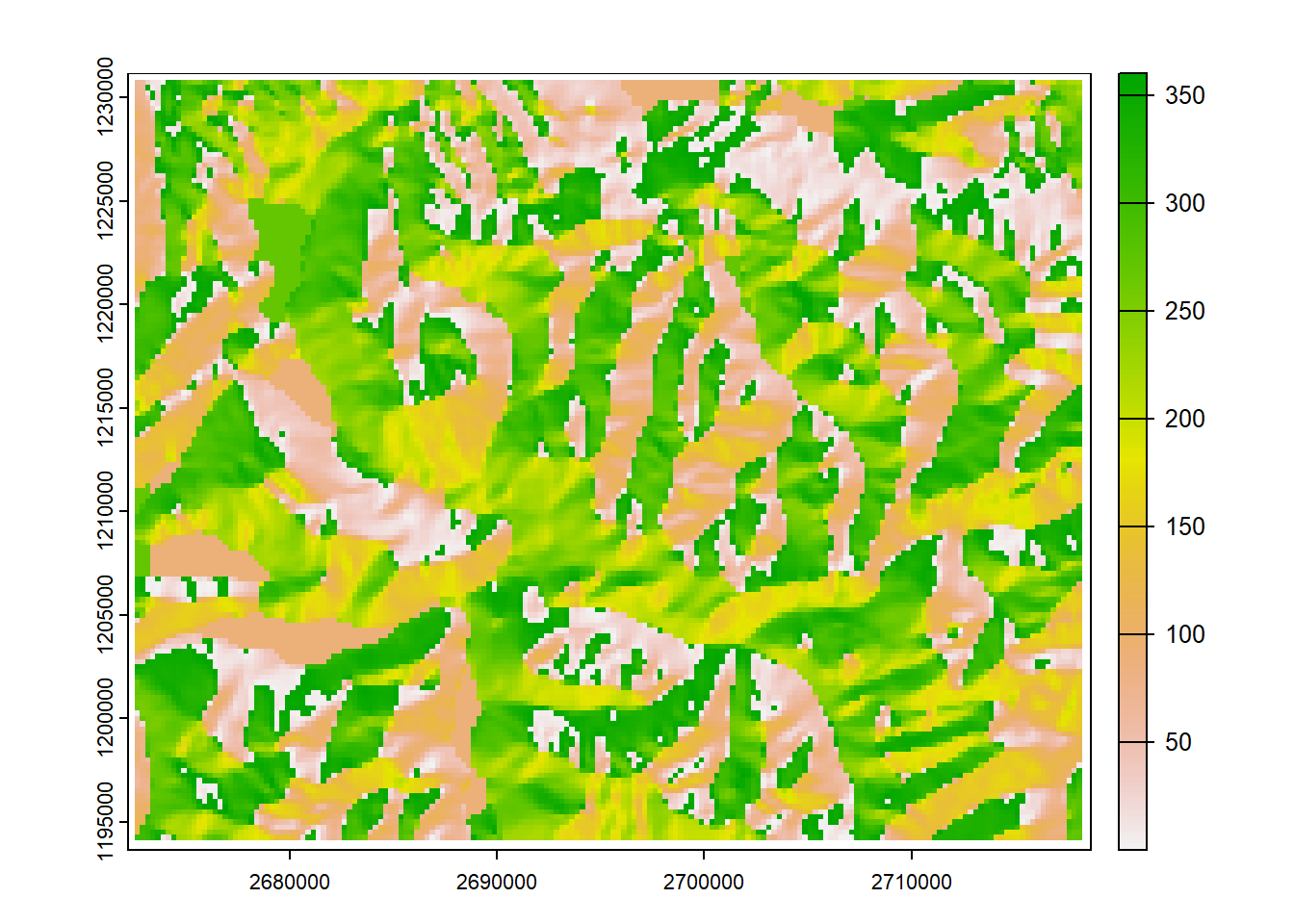
Bei “aspect” handelt es sich ja um Werte, die von 0 bis 360 reichen. In klassischen Palettes liegen die beiden Extremwerte (in diesem Fall 0 und 360) farblich weit auseinander. Bei Aspect sollten diese aber nahe beieinander liegen (da eine Ausrichtung von 1° nur 2 Grad von einer Ausrichtung von 359° entfernt ist). Um dieser Tatsache Rechnung zu Tragen können wir eine eine eigene Colourpalette erstellen, wo die erste Farbe wiederholt ist.
Code
tm_shape(schwyz_aspect) +
tm_raster(
palette = c("#EF476F", "#FFD166", "#06D6A0", "#118AB2", "#EF476F"),
style = "cont", breaks = seq(0, 360, 90)
)
Aufgabe 3
Mit Hangneigung und -ausrichtung können wir einen Hillshading-Effekt berechnen. Hillshading bedeutet, dass der Schattenwurf des Oberflächenmodells bei gegebenen Einfallswinkel der Sonne (Höhe und Azimut) berechnet wird. Der typische Einfallswinkel liegt bei 45° über dem Horizont und von Nordwesten bei 315°.
Um einen Hillshading Effekt zu erzeugen, berechne zuerst slope und aspect von dhm_schwyz analog der letzten Aufgabe, achte aber darauf das die Einheit radians entspricht. Nutze diese beiden Objekte in der Funktion shade() um den Hillshade zu berechnen. Visualisiere den Output anschliessend mit plot oder tmap.
Code
dhm_slope <- terrain(dhm_schwyz, "slope", unit = "radians")
dhm_aspect <- terrain(dhm_schwyz, "aspect", unit = "radians")
dhm_hillshade <- shade(dhm_slope, dhm_aspect, 45, 315)
tm_shape(dhm_hillshade) +
tm_raster(style = "cont", palette = "cividis", legend.show = FALSE) +
tm_layout(frame = FALSE)
tmap und als colour palette cividis