BiEc4_N Multivariate Modelle

Einstieg Multivariate Modelle / Habitatselektionsmodell

Libraries laden

library("sf")
library("terra")
library("dplyr")
library("readr")
library("ggplot2")
library("PerformanceAnalytics")
library("pastecs")
library("car")
library("psych")

Aufgabe 1

Einlesen des Gesamtdatensatzes für die Multivariate Analyse von Moodle

Sichtung des Datensatzes, der Variablen und der Datentypen
Kontrolle wieviele Rehe in diesem Datensatz enthalten sind

Code

DF_mod <- read_delim("datasets/fallstudie_n/Aufgabe4_Datensatz_Habitatnutzung_Modelle_231027_moodle.csv", delim = ";")

str(DF_mod)

class(DF_mod$time_of_day)

table(DF_mod$id)

DF_mod |>
  group_by(id) |>
  summarize(anzahl = n())

length(unique(DF_mod$id))

Aufgabe 2

Unterteilung des Datensatzes in Teildatensätze entsprechend der Tageszeit

Code

DF_mod_night <- DF_mod |>
  filter(time_of_day == "night")

DF_mod_day <- DF_mod |>
  filter(time_of_day == "day")

# Kontrolle
table(DF_mod_night$time_of_day)
## 
## night 
##  3964

table(DF_mod_day$time_of_day)
## 
##  day 
## 3964

Aufgabe 3

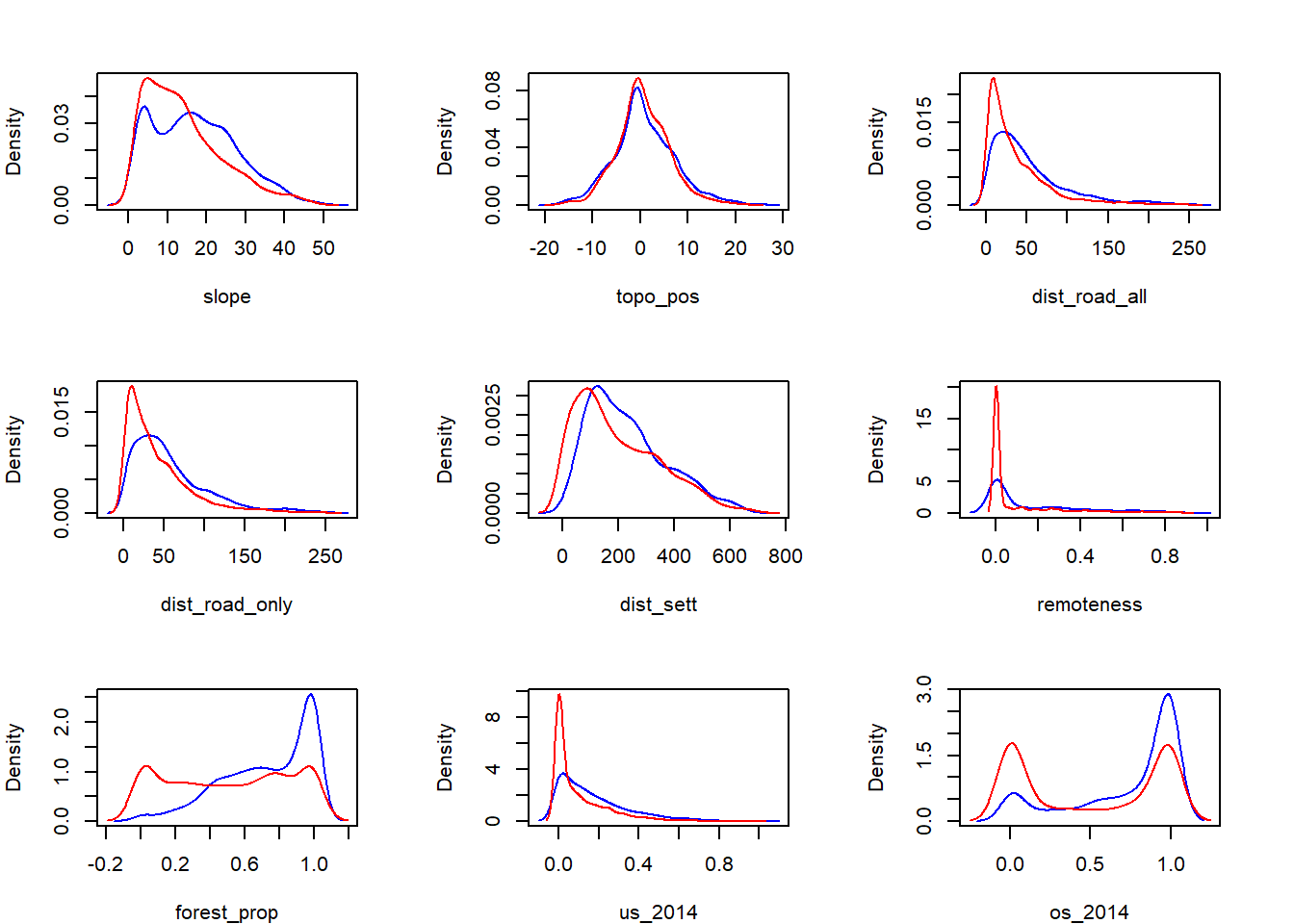
Erstellen von Density Plots der Präsenz / Absenz in Abhängigkeit der unabhängigen Variablen. Diese Übung dient einer ersten groben Einschätzung der Wirkung der Umweltvariablen auf die abhängige Variable (Präsenz/Absenz in unserem Fall)

# Ein Satz Density Plots für den Tagesdatensatz und einer für den Nachtdatensatz

par(mfrow = c(3, 3), mar = c(4, 4, 3, 3)) # Vorbereitung Raster für Plots

# innerhalb des for()-loops die Nummern der gewünschten Spalten einstellen

for (i in 6:14) {
  dp <- DF_mod_day |> filter(pres_abs == 1) |> pull(i)
  dp <- density(dp)
  da <- DF_mod_day |> filter(pres_abs == 0) |> pull(i)
  da <- density(da)
  plot(0, 0, type = "l",
    xlim = range(c(dp$x, da$x)),
    ylim = range(dp$y, da$y),
    xlab = names(DF_mod_day[i]),
    ylab = "Density"
  )
  lines(dp$x, dp$y, col = "blue")             # Präsenz
  lines(da$x, da$y, col = "red")              # Absenz
}

Aufgabe 4

Testen eurer erklärenden Variablen auf Normalverteilung (nur kontinuierliche)

Code

# klassischer Weg mit shapiro-wilk (mehrere Spalten, verschiedenene statistische
# Kenngrössen werden angezeigt. Normalverteilung: Wert ganz unten. p>0.05 = ja)

stat.desc(DF_mod_day[6:14], basic = F, norm = T)
##                      slope     topo_pos dist_road_all dist_road_only
## median        1.370633e+01 2.327148e-01  2.986606e+01   3.505609e+01
## mean          1.535619e+01 7.331813e-01  4.261936e+01   4.765685e+01
## SE.mean       1.629186e-01 9.339098e-02  6.676922e-01   6.901438e-01
## CI.mean.0.95  3.194122e-01 1.830989e-01  1.309052e+00   1.353070e+00
## var           1.052144e+02 3.457351e+01  1.767202e+03   1.888047e+03
## std.dev       1.025741e+01 5.879925e+00  4.203811e+01   4.345166e+01
## coef.var      6.679657e-01 8.019742e+00  9.863616e-01   9.117611e-01
## skewness      7.330597e-01 2.782704e-01  1.872269e+00   1.631521e+00
## skew.2SE      9.424641e+00 3.577606e+00  2.407098e+01   2.097578e+01
## kurtosis     -9.231943e-02 7.476704e-01  4.033217e+00   2.994463e+00
## kurt.2SE     -5.936055e-01 4.807452e+00  2.593322e+01   1.925412e+01
## normtest.W    9.419360e-01 9.902728e-01  8.067698e-01   8.431235e-01
## normtest.p    6.839535e-37 7.269676e-16  2.675211e-56   1.245661e-52
##                  dist_sett   remoteness   forest_prop      us_2014
## median        1.809658e+02 0.000000e+00  6.554673e-01 5.882353e-02
## mean          2.119112e+02 1.188578e-01  5.976772e-01 1.194621e-01
## SE.mean       2.358616e+00 3.228686e-03  5.272256e-03 2.386145e-03
## CI.mean.0.95  4.624214e+00 6.330041e-03  1.033659e-02 4.678188e-03
## var           2.205200e+04 4.132237e-02  1.101861e-01 2.256978e-02
## std.dev       1.484992e+02 2.032790e-01  3.319428e-01 1.502324e-01
## coef.var      7.007614e-01 1.710270e+00  5.553882e-01 1.257574e+00
## skewness      7.209630e-01 1.808899e+00 -4.046525e-01 1.647457e+00
## skew.2SE      9.269118e+00 2.325625e+01 -5.202447e+00 2.118066e+01
## kurtosis     -1.740088e-01 2.374388e+00 -1.115659e+00 2.923840e+00
## kurt.2SE     -1.118861e+00 1.526710e+01 -7.173587e+00 1.880002e+01
## normtest.W    9.452976e-01 6.538165e-01  9.104534e-01 7.934120e-01
## normtest.p    4.868489e-36 3.078496e-67  2.141161e-43 1.674851e-57
##                    os_2014
## median        7.847363e-01
## mean          5.939976e-01
## SE.mean       6.653214e-03
## CI.mean.0.95  1.304404e-02
## var           1.754675e-01
## std.dev       4.188884e-01
## coef.var      7.052022e-01
## skewness     -4.252236e-01
## skew.2SE     -5.466921e+00
## kurtosis     -1.571720e+00
## kurt.2SE     -1.010602e+01
## normtest.W    7.807897e-01
## normtest.p    1.397443e-58

# empfohlener Weg

ggplot(DF_mod_day, aes(slope)) +
  geom_histogram(aes(y = after_stat(density)), color = "black", fill = "white") +
  stat_function(fun = dnorm, args = list(mean = mean(DF_mod_day$slope, na.rm = T), sd = sd(DF_mod_day$slope, na.rm = T)), color = "black", size = 1)

Code

# Aufgabe 4: die Verteilung bei einem Teildatensatz zu testen reicht,
# denn die verwendeten Kreise sind die selben am Tag und in der Nacht,
# nur die Nutzung durch das Reh nicht

Aufgabe 5

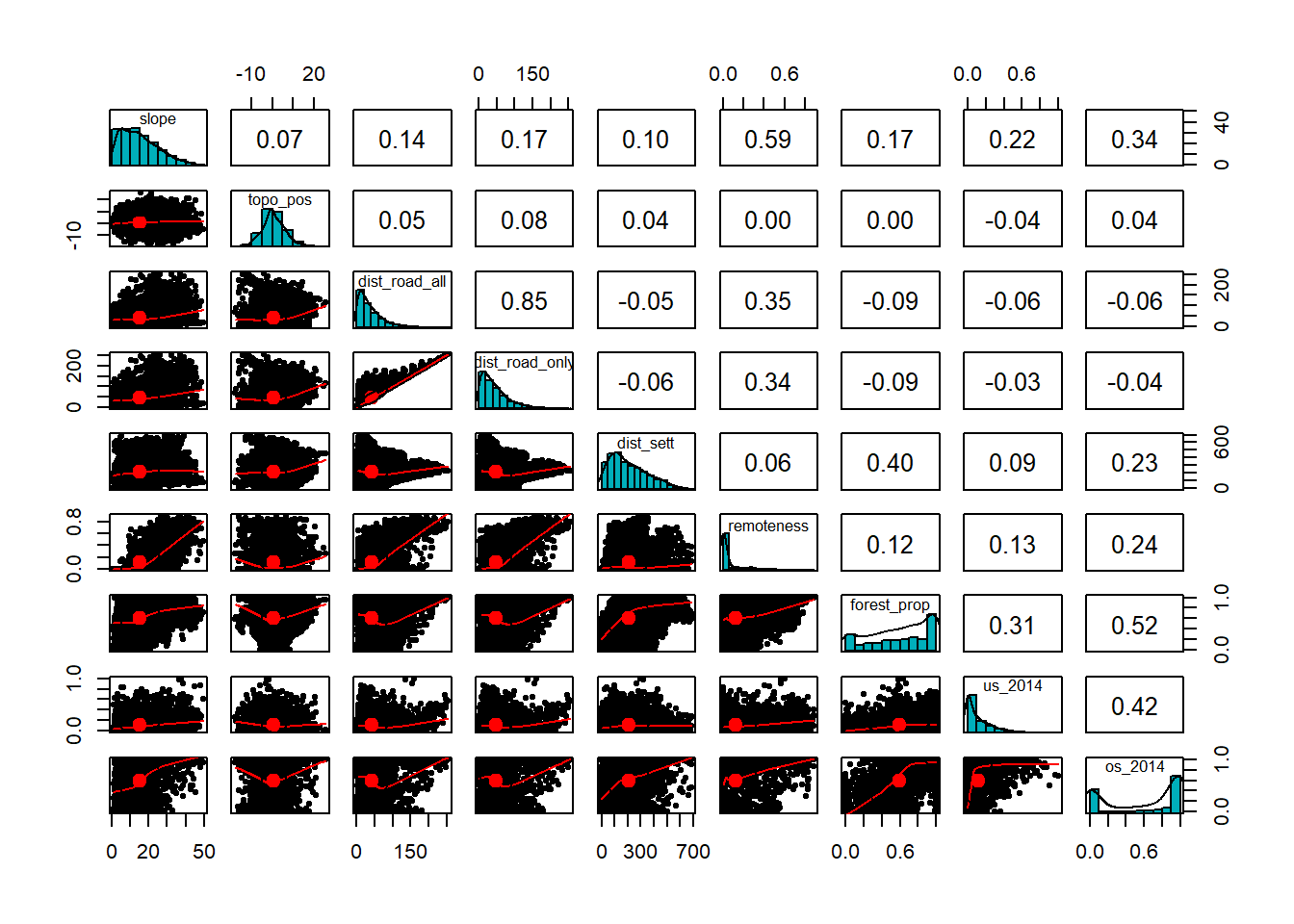
Explorative Analysen der Variablen mit Scatterplots / Scatterplotmatrizen

Zu Scatterplots und Scatterplotmatrizen gibt es viele verschiedene Funktionen / Packages, schaut im Internet und sucht euch eines welches euch passt.
Testen der Korrelation zwischen den Variablen (Parametrisch oder nicht-parametrische Methode? Ausserdem: gewisse Scatterplotmatrizen zeigen euch die Koeffizenten direkt an)

Code

chart.Correlation(DF_mod_day[6:14], histogram = TRUE, pch = 19, method = "kendall")

Code


# ?chart.Correlation

pairs.panels(DF_mod_day[6:14],
  method = "kendall", # correlation method
  hist.col = "#00AFBB",
  density = TRUE, # show density plots
  ellipses = TRUE # show correlation ellipses
)

Code


# Aufgabe 5: die Korrelation bei einem Teildatensatz zu testen reicht,
# denn die verwendeten Kreise sind die selben am Tag und in der Nacht,
# nur die Nutzung durch das Reh nicht.