BiEc3_N Homeranges

Libraries laden

library("sf")
library("terra")
library("dplyr")
library("readr")
library("ggplot2")
library("terra")
library("adehabitatHR")
library("ggspatial")

Daten einlesen

Einlesen des Gesamtdatensatzes von Moodle, Sichtung des Datensatzes und der Datentypen

Rehe <- read_delim("datasets/fallstudie_n/Aufgabe3_Homeranges_Rehe_landforst_20231023.csv", delim = ";")

str(Rehe)

Aufgabe 1

Im Datensatz Rehe eine neue Spalte mit Datum und Zeit in einer Spalte kreieren. Beim Format hat sich ein Fehler eingeschlichen. Findet ihr ihn?

Rehe <- Rehe |>
  mutate(UTC_DateTime = as.POSIXct(paste(UTC_Date, UTC_Time),
                                   format = "%Y-%m-%d %H:%M:%S"))

Aufgabe 2

Mit den folgenden Zeilen können die GPS-Punkte visualisiert werden

Rehe_sf <- st_as_sf(Rehe, coords = c("X", "Y"), crs = 21781)

RE13 <- filter(Rehe_sf, TierID == "RE13")

plot(RE13["TierID"])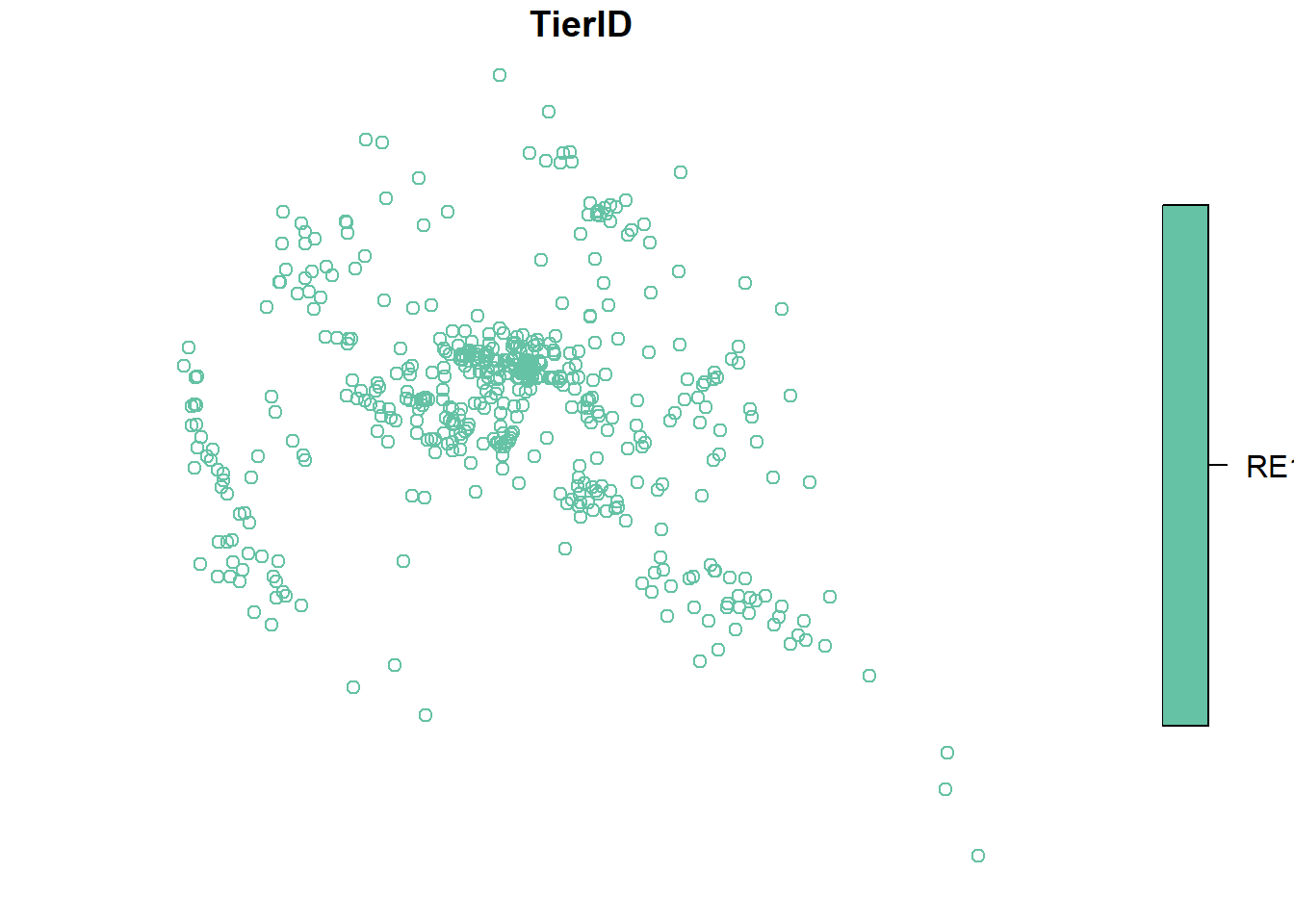

Hier einige Zeilen Code, um eine HomeRange zu berechnen.

Herumschrauben an der Ausdehnung, resp. prozentualer Anteil Punkte in der HR (Funktion getverticeshr)

→ Ziel: eine Karte erstellen mit der Visualiserung mindestens einer HR

RE13_xy <- st_coordinates(RE13)

RE13_sp <- as(RE13["TierID"], "Spatial")

sigma <- 0.5 * (sd(RE13_xy[, 1]) + sd(RE13_xy[, 2]))
n <- nrow(RE13)
href <- sigma * n ^ (-1 / 6) * 0.9

# scaled reference: href * 0.9

kud <- kernelUD(RE13_sp, h = href, grid = 25)

# Berechnung der Home Range (95% Isopleth)

homerange <- getverticeshr(kud, percent = 95)

# Schreibt HR in den oben beschriebenen Ordner (als Shapefile)

hr <- st_as_sf(homerange)

st_write(
  hr,
  dsn = "Results",
  layer = "HR_RE13",
  driver = "ESRI Shapefile",
  delete_layer = TRUE
)
## Deleting layer `HR_RE13' using driver `ESRI Shapefile'
## Writing layer `HR_RE13' to data source `Results' using driver `ESRI Shapefile'
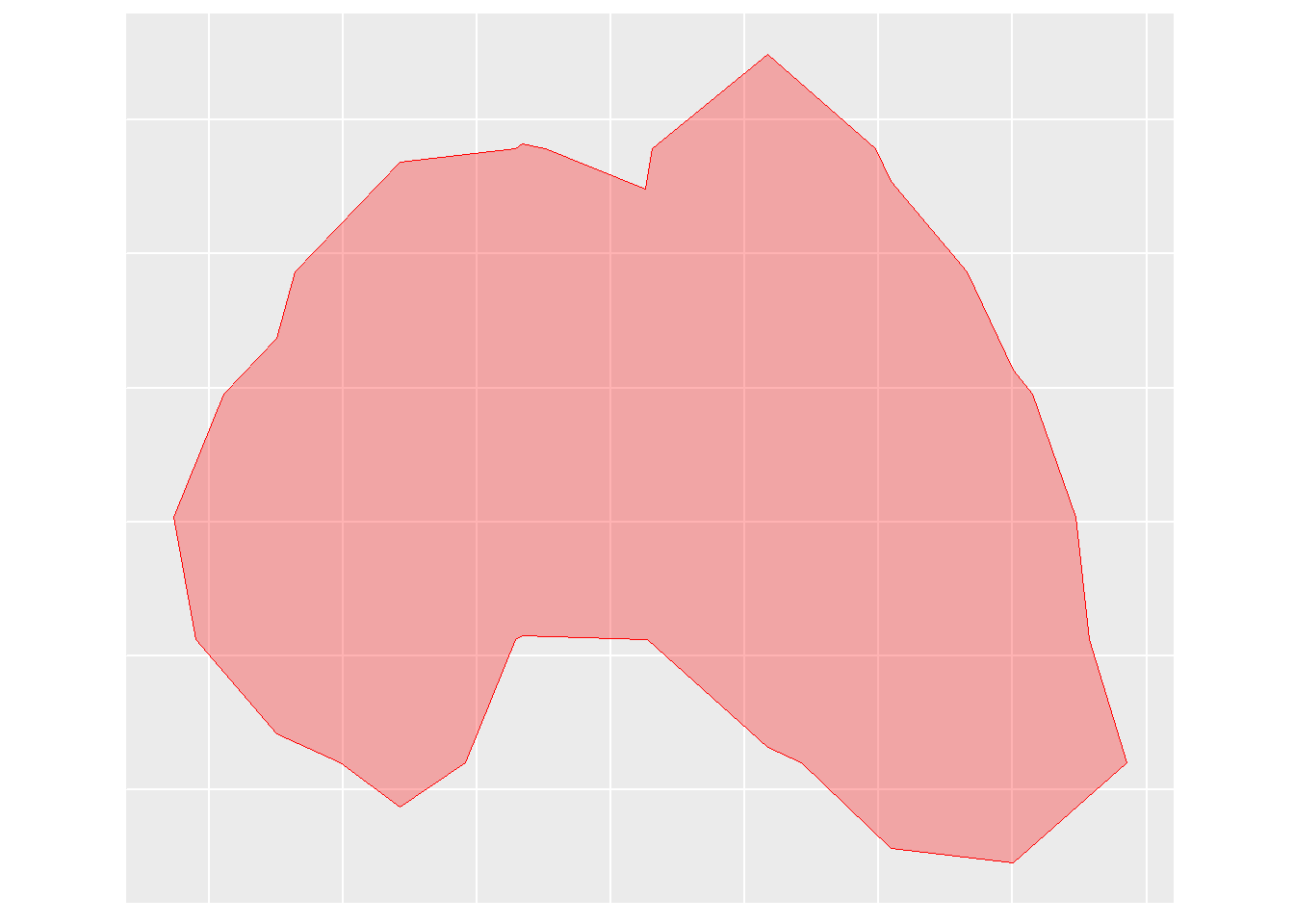
## Writing 1 features with 2 fields and geometry type Polygon.

# mit diesem Befehl kann die HR geplottet werden

ggplot(hr) + 
  geom_sf(size = 1, alpha = 0.3, color = "red", fill="red") +
  coord_sf(datum = sf::st_crs(21781))+
  theme(
    axis.title = element_blank(),
    axis.text = element_blank(),
    axis.ticks = element_blank(),
    legend.position="none"
  )

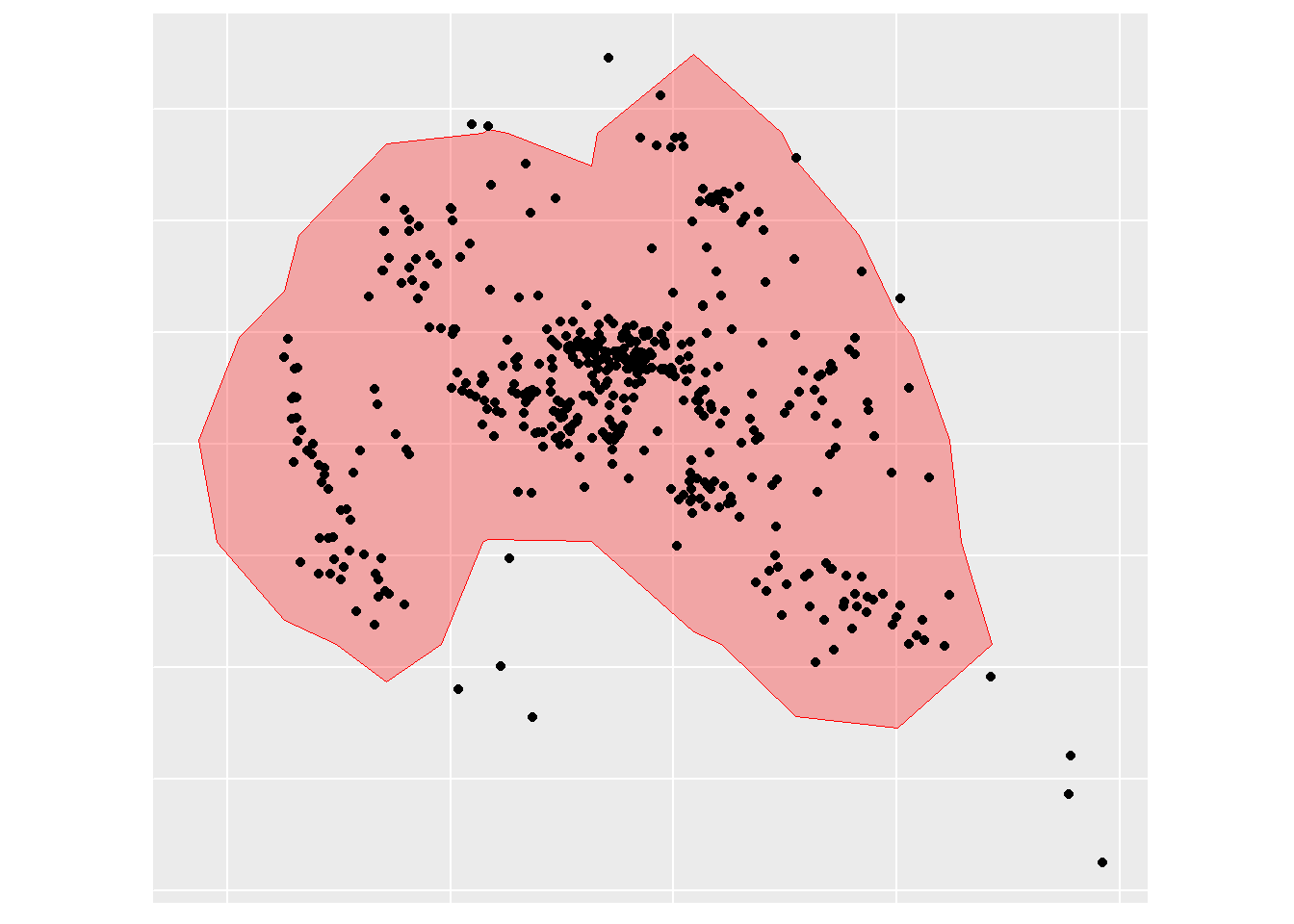
# und die Punkte der GPS-Lokalisationen darüber gelegt werden 

ggplot(hr) + 
  geom_sf(size = 1, alpha = 0.3, color = "red", fill="red") +
  geom_sf(data = RE13, aes(fill = "red")) +
  coord_sf(datum = sf::st_crs(21781))+
  theme(
    axis.title = element_blank(),
    axis.text = element_blank(),
    axis.ticks = element_blank(),
    legend.position="none"
  )

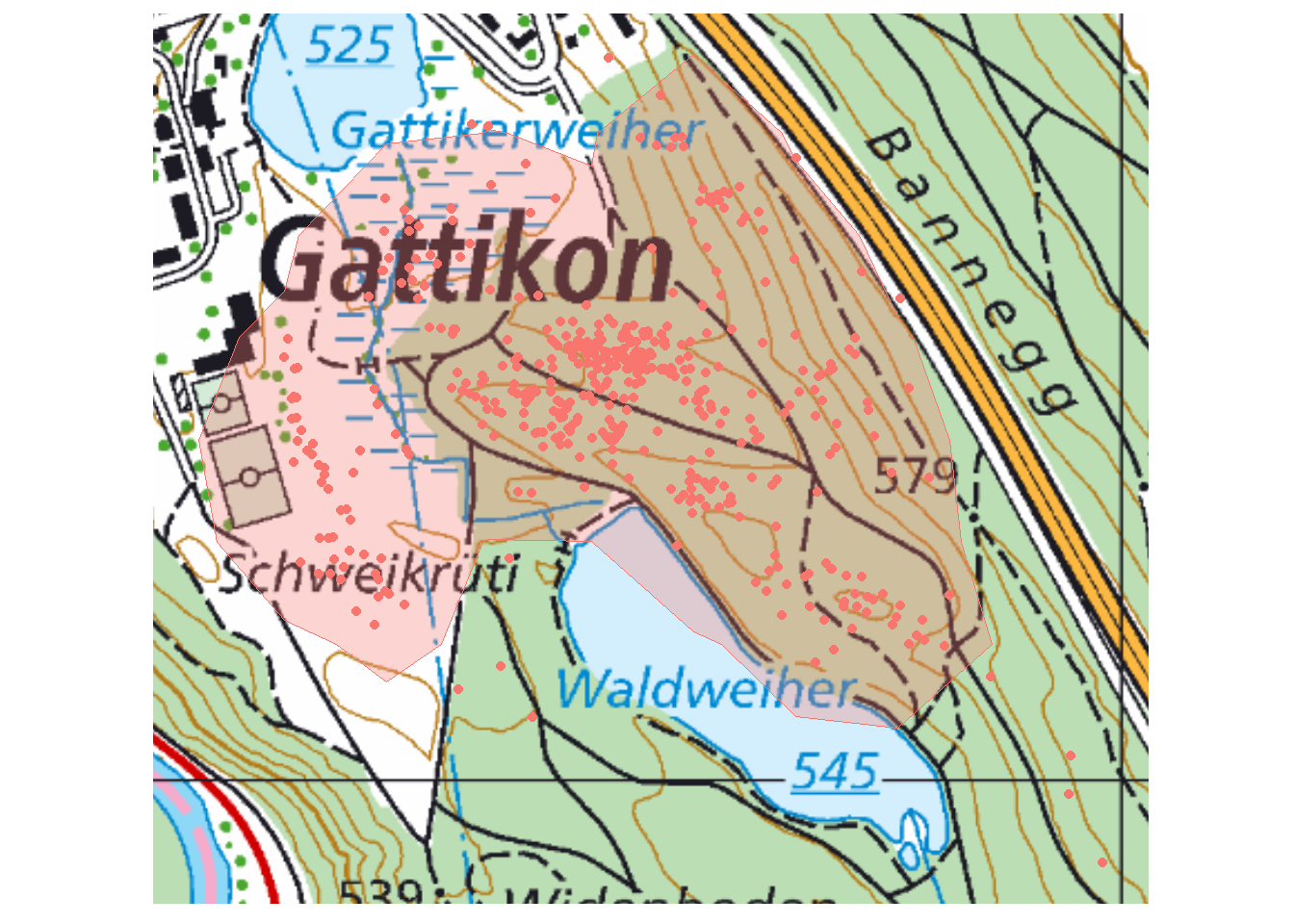
Code um die Homerange auf der Landeskarte 1:25000 zu plotten. Transparenz kann mit alpha angepasst werden.

pk25_wpz <- rast("datasets/fallstudie_n/pk25_wpz.tif")

ggplot(hr, aes(color = "red", fill = "red")) +
  annotation_spatial(pk25_wpz) +
  geom_sf(size = 1, alpha = 0.3) +
  geom_sf(data = RE13, aes(fill = "red")) +
  coord_sf(datum = sf::st_crs(21781)) +
  theme(
    axis.title = element_blank(),
    axis.text = element_blank(),
    axis.ticks = element_blank(),
    legend.position = "none"
  )

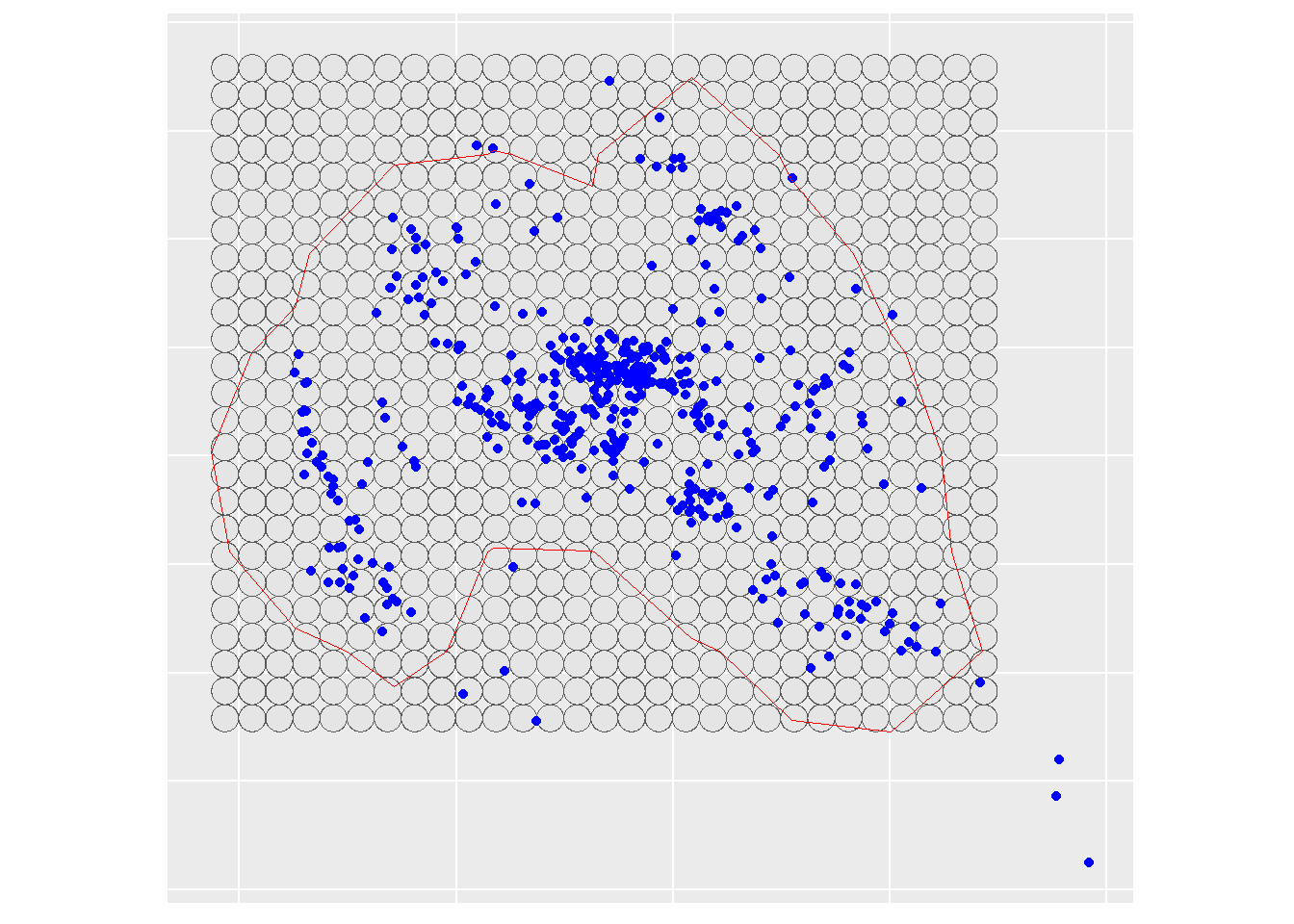
Nachbauen des Sampling Grids mit den Kreisen (Wird als Grundlage für Extraktion der Umweltvariablen innerhalb der Homeranges benötigt)

• Ausdehnung des Grids basiert auf hr
• Cellsize des Grids: 25m

x25 <- st_make_grid(hr, 25, what = "centers")
grid_plot <- st_buffer(x25, 12.5)

ggplot(grid_plot, color = "black", fill = NA) +
  geom_sf() +
  geom_sf(data = RE13, color = "blue", ) +
  geom_sf(data = hr, color = "red", fill = NA, size = 2) +
  coord_sf(datum = 21781) +
  theme(
    axis.title = element_blank(),
    axis.text = element_blank(),
    axis.ticks = element_blank(),
    legend.position = "none"
  )

Aufgabe 3

Testen der Variablen der Vegetationsschichten von letzter Woche auf einen linearen Zusammenhang (Korrelation; Funktion cor.test). DG_Baumschicht vs. DG_os / DG_Strauchschicht vs. DG_us aus dem Datensatz df_with_lidar den wir letzte Woche erstellt haben

Die Theorie zu Korrelation folgt erst ab 31.10.

df_with_lidar <- read_delim("datasets/fallstudie_n/df_with_lidar.csv", delim = ";")

cor.test(~ DG_Strauchschicht + DG_us_2022, data = df_with_lidar, method = "pearson")
## 
##  Pearson's product-moment correlation
## 
## data:  DG_Strauchschicht and DG_us_2022
## t = 4.8012, df = 123, p-value = 4.49e-06
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  0.2382939 0.5355237
## sample estimates:
##       cor 
## 0.3972769