library("readr")
library("ggplot2")
library("tibble")Statistik 8: Übung
- Datensatz crime.csv
Raten von 7 Kriminalitätsformen pro 100000 Einwohner und Jahr für die Bundesstaaten der USA
- (a) Führt eine k-means- Clusteranalyse durch.
- (b) Überlegt bzw testet wieviele Cluster sinnvoll sind
- (c) Abschliessend entscheidet euch für eine Clusterung und vergleicht die erhaltenen Cluster bezüglich der Kriminalitätsformen mittels ANOVA und interpretiert die Cluster entsprechend.
Hinweis: Wegen der sehr ungleichen Varianzen muss auf jeden Fall eine Standardisierung stattfinden, damit Distanzen zwischen den verschiedenen Kriminalitätsraten sinnvoll berechnet werden können
- Bitte erklärt und begründet die einzelnen Schritte, die ihr unternehmt, um zu diesem Ergebnis zu kommen. Dazu erstellt bitte ein mit Quarto generiertes pdf-Dokument, in das ihr Schritt für Schritt den verwendeten R-Code, die dazu gehörigen Ausgaben von R, eure Interpretation derselben und die sich ergebenden Schlussfolgerungen für das weitere Vorgehen dokumentieren.
- Formuliert abschliessend einen Methoden- und Ergebnisteil (ggf. incl. adäquaten Abbildungen) zu dieser Untersuchung in der Form einer wissenschaftlichen Arbeit (ausformulierte schriftliche Zusammenfassung, mit je einem Absatz von ca. 60-100 Worten, resp. 3-8 Sätzen für den Methoden- und Ergebnisteil). D. h. alle wichtigen Informationen sollten enthalten sein, unnötige Redundanz dagegen vermieden werden.
- Zu erstellen sind (a) Ein quarto generiertes html-Dokument mit begründetem Lösungsweg (Kombination aus R-Code, R Output und dessen Interpretation) und (b) ausformulierter Methoden- und Ergebnisteil
Demoscript herunterladen (.qmd)
crime <-
read_delim("./datasets/stat/crime.csv", delim = ";", col_names = TRUE) |>
column_to_rownames(var = "State")
str(crime)'data.frame': 50 obs. of 7 variables:
$ Murder : num 2 2.2 2 3.6 3.5 4.6 10.7 5.2 5.5 5.5 ...
$ Rape : num 14.8 21.5 21.8 29.7 21.4 23.8 30.5 33.2 25.1 38.6 ...
$ Robbery : num 28 24 22 193 119 192 514 269 152 142 ...
$ Assault : num 102 92 103 331 192 205 431 265 176 235 ...
$ Burglary: num 803 755 949 1071 1294 ...
$ Theft : num 2347 2208 2697 2189 2568 ...
$ Vehicle : num 164 228 181 906 705 447 637 776 354 376 ...summary(crime) Murder Rape Robbery Assault
Min. : 1.000 Min. :11.60 Min. : 7.0 Min. : 32.0
1st Qu.: 3.700 1st Qu.:23.27 1st Qu.: 67.0 1st Qu.:176.5
Median : 6.300 Median :30.10 Median :109.5 Median :248.0
Mean : 6.776 Mean :33.85 Mean :142.1 Mean :275.7
3rd Qu.: 9.275 3rd Qu.:43.45 3rd Qu.:202.8 3rd Qu.:366.0
Max. :13.500 Max. :72.70 Max. :514.0 Max. :605.0
Burglary Theft Vehicle
Min. : 385 Min. :1358 Min. : 99.0
1st Qu.: 894 1st Qu.:2366 1st Qu.:209.8
Median :1148 Median :2812 Median :328.0
Mean :1197 Mean :2918 Mean :382.2
3rd Qu.:1425 3rd Qu.:3382 3rd Qu.:529.5
Max. :2221 Max. :4373 Max. :906.0 crimez <- scale(crime)„scale“ führt eine Standardisierung (z-Transformation) durch, so dass alle Variablen anschiessend einen Mittelwert von 0 und eine SD von 1 haben. Anschliessend wird das SSI-Kriterium getestet und zwar für Partitionierungen von 2 bis 6 Gruppen (wie viele Gruppen man maximal haben will, muss man pragmatisch nach der jeweiligen Fragestelltung entscheiden).
library("vegan")
set.seed(123)
km_cascade <- cascadeKM(crimez, inf.gr = 2, sup.gr = 6, iter = 100, criterion = "ssi")
km_cascade$results 2 groups 3 groups 4 groups 5 groups 6 groups
SSE 174.959159 144.699605 124.437221 108.119280 95.446705
ssi 1.226057 1.304674 1.555594 1.539051 1.507395km_cascade$partition 2 groups 3 groups 4 groups 5 groups 6 groups
ME 2 3 3 2 1
NH 2 3 3 2 1
VT 2 3 3 2 1
MA 1 1 2 1 6
RI 2 1 4 1 6
CT 2 1 4 1 6
NY 1 1 2 4 4
NJ 1 1 2 1 6
PA 2 3 4 5 3
OH 2 1 4 5 2
IN 2 3 4 5 3
IL 1 1 2 4 4
MI 1 2 1 4 4
WI 2 3 3 2 1
MN 2 3 3 2 1
IA 2 3 3 2 1
MO 1 1 4 5 2
ND 2 3 3 2 1
SD 2 3 3 2 3
NE 2 3 3 2 1
KS 2 3 4 5 1
DE 2 1 4 5 2
MD 1 1 2 4 4
VA 2 3 4 5 3
WV 2 3 3 2 3
NC 2 1 4 5 2
SC 1 1 4 5 2
GA 1 1 1 4 2
FL 1 2 1 4 4
KY 2 3 4 5 3
TN 1 1 2 5 2
AL 2 1 4 5 2
MS 2 3 4 5 3
AR 2 3 4 5 3
LA 1 2 1 4 4
OK 1 1 1 3 5
TX 1 2 1 4 4
MT 2 3 3 2 1
ID 2 3 3 2 1
WY 2 3 3 2 1
CO 1 2 1 3 5
NM 1 2 1 3 5
AZ 1 2 1 3 5
UT 2 3 3 2 1
NV 1 2 1 4 4
WA 1 2 1 3 5
OR 1 2 1 3 5
CA 1 2 1 4 4
AK 1 2 1 3 5
HI 2 3 4 2 1# k-means visualisation
library("cclust")
plot(km_cascade, sortg = TRUE)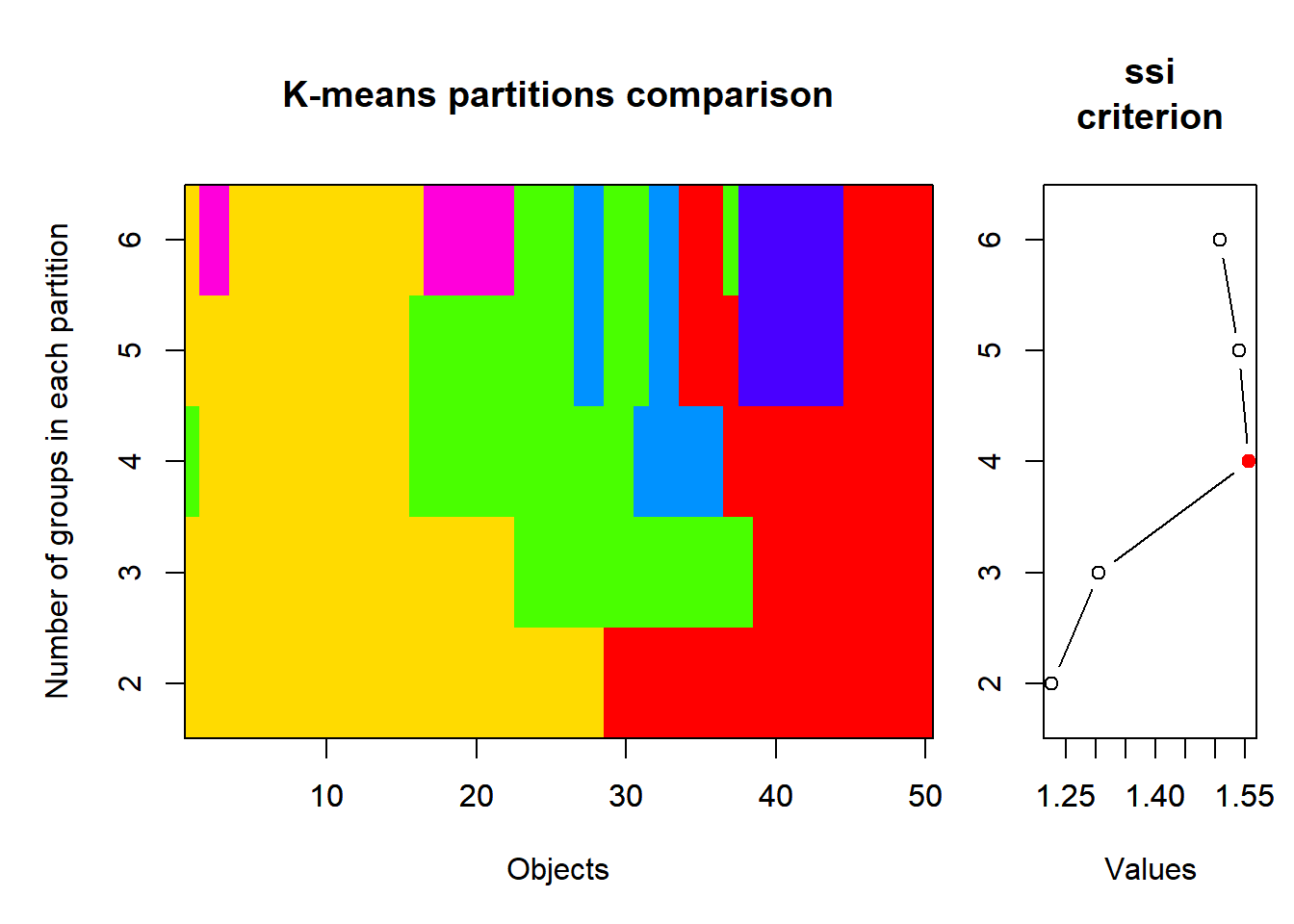
Nach SSI ist die 4-Gruppenlösung die beste, mit dieser wird also weitergerechnet.
# 4 Kategorien sind nach SSI offensichtlich besonders gut
set.seed(123)
kmeans_1 <- kmeans(crimez, 4, nstart = 100)
kmeans_1K-means clustering with 4 clusters of sizes 14, 16, 14, 6
Cluster means:
Murder Rape Robbery Assault Burglary Theft
1 -1.088869933 -0.9575423 -0.9573223 -1.0018455 -0.966220768 -0.3729397
2 -0.002098593 -0.2436615 -0.2668763 -0.1457373 -0.279054485 -0.5371659
3 0.943560464 1.1705377 0.6331926 0.8825420 1.287858358 1.1323972
4 0.344651676 0.1527746 1.4679727 0.6670075 -0.006342418 -0.3396250
Vehicle
1 -0.9310433
2 -0.3276196
3 0.7120264
4 1.3846917
Clustering vector:
ME NH VT MA RI CT NY NJ PA OH IN IL MI WI MN IA MO ND SD NE KS DE MD VA WV NC
1 1 1 4 2 2 4 4 2 2 2 4 3 1 1 1 2 1 1 1 2 2 4 2 1 2
SC GA FL KY TN AL MS AR LA OK TX MT ID WY CO NM AZ UT NV WA OR CA AK HI
2 3 3 2 4 2 2 2 3 3 3 1 1 1 3 3 3 1 3 3 3 3 3 2
Within cluster sum of squares by cluster:
[1] 19.37307 39.51883 48.95481 16.59050
(between_SS / total_SS = 63.7 %)
Available components:
[1] "cluster" "centers" "totss" "withinss" "tot.withinss"
[6] "betweenss" "size" "iter" "ifault" kmeans_1$size[1] 14 16 14 6# Clustering-Resultat in Ordinationsplots darstellen
library(factoextra)
fviz_cluster(kmeans_1, data = crimez) +
theme_classic() +
theme(plot.title = element_blank())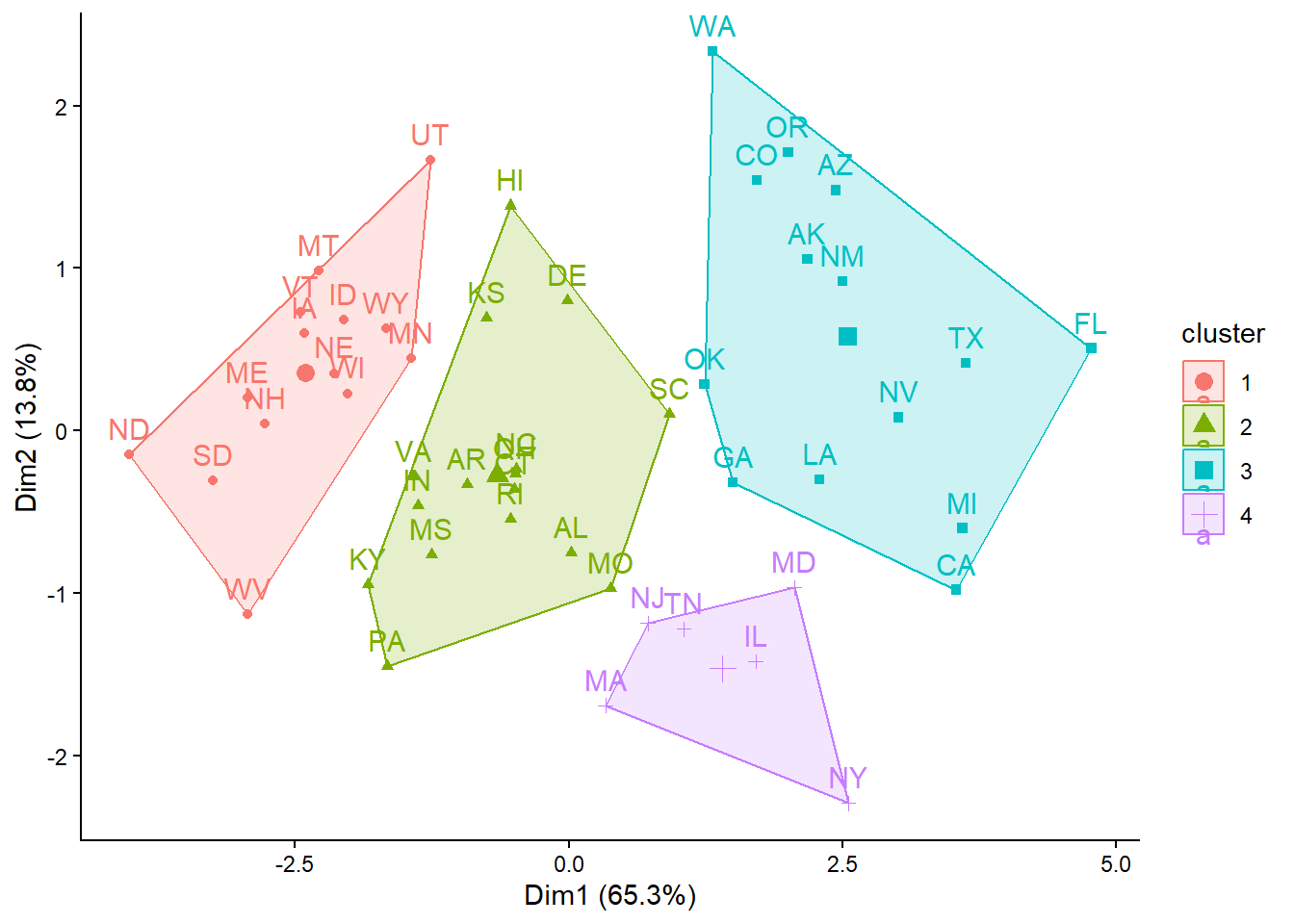
# File für ANOVA (Originaldaten der Vorfälle, nicht die ztransformierten)
crime_KM4 <- data.frame(crime, kmeans_1[1])
crime_KM4$cluster <- as.factor(crime_KM4$cluster)
crime_KM4 Murder Rape Robbery Assault Burglary Theft Vehicle cluster
ME 2.0 14.8 28 102 803 2347 164 1
NH 2.2 21.5 24 92 755 2208 228 1
VT 2.0 21.8 22 103 949 2697 181 1
MA 3.6 29.7 193 331 1071 2189 906 4
RI 3.5 21.4 119 192 1294 2568 705 2
CT 4.6 23.8 192 205 1198 2758 447 2
NY 10.7 30.5 514 431 1221 2924 637 4
NJ 5.2 33.2 269 265 1071 2822 776 4
PA 5.5 25.1 152 176 735 1654 354 2
OH 5.5 38.6 142 235 988 2574 376 2
IN 6.0 25.9 90 186 887 2333 328 2
IL 8.9 32.4 325 434 1180 2938 628 4
MI 11.3 67.4 301 424 1509 3378 800 3
WI 3.1 20.1 73 162 783 2802 254 1
MN 2.5 31.8 102 148 1004 2785 288 1
IA 1.8 12.5 42 179 956 2801 158 1
MO 9.2 29.2 170 370 1136 2500 439 2
ND 1.0 11.6 7 32 385 2049 120 1
SD 4.0 17.7 16 87 554 1939 99 1
NE 3.1 24.6 51 184 748 2677 168 1
KS 4.4 32.9 80 252 1188 3008 258 2
DE 4.9 56.9 124 241 1042 3090 272 2
MD 9.0 43.6 304 476 1296 2978 545 4
VA 7.1 26.5 106 167 813 2522 219 2
WV 5.9 18.9 41 99 625 1358 169 1
NC 8.1 26.4 88 354 1225 2423 208 2
SC 8.6 41.3 99 525 1340 2846 277 2
GA 11.2 43.9 214 319 1453 2984 430 3
FL 11.7 52.7 367 605 2221 4373 598 3
KY 6.7 23.1 83 222 824 1740 193 2
TN 10.4 47.0 208 274 1325 2126 544 4
AL 10.1 28.4 112 408 1159 2304 267 2
MS 11.2 25.8 65 172 1076 1845 150 2
AR 8.1 28.9 80 278 1030 2305 195 2
LA 12.8 40.1 224 482 1461 3417 442 3
OK 8.1 36.4 107 285 1787 3142 649 3
TX 13.5 51.6 240 354 2049 3987 714 3
MT 2.9 17.3 20 118 783 3314 215 1
ID 3.2 20.0 21 178 1003 2800 181 1
WY 5.3 21.9 22 243 817 3078 169 1
CO 7.0 42.3 145 329 1792 4231 486 3
NM 11.5 46.9 130 538 1845 3712 343 3
AZ 9.3 43.0 169 437 1908 4337 419 3
UT 3.2 25.3 59 180 915 4074 223 1
NV 12.6 64.9 287 354 1604 3489 478 3
WA 5.0 53.4 135 244 1861 4267 315 3
OR 6.6 51.1 206 286 1967 4163 402 3
CA 11.3 44.9 343 521 1696 3384 762 3
AK 8.6 72.7 88 401 1162 3910 604 3
HI 4.8 31.0 106 103 1339 3759 328 2str(crime_KM4)'data.frame': 50 obs. of 8 variables:
$ Murder : num 2 2.2 2 3.6 3.5 4.6 10.7 5.2 5.5 5.5 ...
$ Rape : num 14.8 21.5 21.8 29.7 21.4 23.8 30.5 33.2 25.1 38.6 ...
$ Robbery : num 28 24 22 193 119 192 514 269 152 142 ...
$ Assault : num 102 92 103 331 192 205 431 265 176 235 ...
$ Burglary: num 803 755 949 1071 1294 ...
$ Theft : num 2347 2208 2697 2189 2568 ...
$ Vehicle : num 164 228 181 906 705 447 637 776 354 376 ...
$ cluster : Factor w/ 4 levels "1","2","3","4": 1 1 1 4 2 2 4 4 2 2 ...Damit die Boxplots und die ANOVA direkt interpretierbar sind, werden für diese, anders als für die Clusterung, die untransformierten Incidenz-Werte verwendet (also crime statt crimez). Die Spalte mit der Clusterzugehörigkeit im Fall von k-means mit 4 Clustern hängt man als Spalte an (Achtung: muss als Faktor definiert werden!).
Anschliessend kann man die 7 ANOVAs rechnen, die Posthoc-Vergleiche durchführen und die zugehörigen Boxplots mit Buchstaben für die homogenen Gruppen erzeugen. Sinnvollerweise gruppiert man die Abbildungen gleich, z. B. je 2 x 2.
library("multcomp")
aov_Murder <- aov(Murder ~ cluster, data = crime_KM4)
summary(aov_Murder) Df Sum Sq Mean Sq F value Pr(>F)
cluster 3 355.4 118.46 23.75 1.96e-09 ***
Residuals 46 229.4 4.99
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1letters <- cld( glht(aov_Murder, linfct = mcp(cluster = "Tukey")))
cld_letters <- data.frame(cluster = names(letters$mcletters$Letters),
letters = letters$mcletters$Letters)
f_Murder <-
ggplot(crime_KM4, aes(x = cluster, y = Murder)) +
geom_boxplot() +
geom_text(data = cld_letters, aes(label = letters, x = c(1:4), y = max(crime_KM4$Murder) * 1.2)) +
ylim(0, max(crime_KM4$Murder) * 1.2) +
theme_classic()
#
aov_Rape <- aov(Rape ~ cluster, data = crime_KM4)
summary(aov_Rape) Df Sum Sq Mean Sq F value Pr(>F)
cluster 3 6945 2315.0 31.95 2.58e-11 ***
Residuals 46 3333 72.5
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1letters <- cld(glht(aov_Rape, linfct = mcp(cluster = "Tukey")))
cld_letters <- data.frame(cluster = names(letters$mcletters$Letters),
letters = letters$mcletters$Letters)
f_Rape <-
ggplot(crime_KM4, aes(x = cluster, y = Rape)) +
geom_boxplot() +
geom_text(data = cld_letters, aes(label = letters, x = c(1:4), y = max(crime_KM4$Rape)* 1.2)) +
ylim(0, max(crime_KM4$Rape) * 1.2) +
theme_classic()
#
aov_Robbery <- aov(Robbery ~ cluster, data = crime_KM4)
summary(aov_Robbery) Df Sum Sq Mean Sq F value Pr(>F)
cluster 3 386563 128854 30.24 5.96e-11 ***
Residuals 46 196025 4261
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1letters <- cld(glht(aov_Robbery, linfct = mcp(cluster = "Tukey")))
cld_letters <- data.frame(cluster = names(letters$mcletters$Letters),
letters = letters$mcletters$Letters)
f_Robbery <-
ggplot(crime_KM4, aes(x = cluster, y = Robbery)) +
geom_boxplot() +
geom_text(data = cld_letters, aes(label = letters, x = c(1:4), y = max(crime_KM4$Robbery) * 1.2)) +
ylim(0, max(crime_KM4$Robbery) * 1.2) +
theme_classic()
#
aov_Assault <- aov(Assault ~ cluster, data = crime_KM4)
summary(aov_Assault) Df Sum Sq Mean Sq F value Pr(>F)
cluster 3 541786 180595 20.39 1.51e-08 ***
Residuals 46 407517 8859
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1letters <- cld(glht(aov_Rape, linfct = mcp(cluster = "Tukey")))
cld_letters <- data.frame(cluster = names(letters$mcletters$Letters),
letters = letters$mcletters$Letters)
f_Ausault <-
ggplot(crime_KM4, aes(x = cluster, y = Assault)) +
geom_boxplot() +
geom_text(data = cld_letters, aes(label = letters, x = c(1:4), y = max(crime_KM4$Assault) * 1.2)) +
ylim(0, max(crime_KM4$Assault) * 1.2) +
theme_classic()
#
aov_Burglary <- aov(Burglary ~ cluster, data = crime_KM4)
summary(aov_Burglary) Df Sum Sq Mean Sq F value Pr(>F)
cluster 3 6602474 2200825 50.21 1.5e-14 ***
Residuals 46 2016382 43834
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1letters <- cld(glht(aov_Burglary, linfct = mcp(cluster = "Tukey")))
cld_letters <- data.frame(cluster = names(letters$mcletters$Letters),
letters = letters$mcletters$Letters)
f_Burglary <-
ggplot(crime_KM4, aes(x = cluster, y = Burglary)) +
geom_boxplot() +
geom_text(data = cld_letters, aes(label = letters, x = c(1:4), y = max(crime_KM4$Burglary)* 1.2)) +
ylim(0, max(crime_KM4$Burglary) * 1.2) +
theme_classic()
#
aov_Theft <- aov(Theft ~ cluster, data = crime_KM4)
summary(aov_Theft) Df Sum Sq Mean Sq F value Pr(>F)
cluster 3 14249791 4749930 16.25 2.44e-07 ***
Residuals 46 13448760 292364
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1letters <- cld(glht(aov_Theft, linfct = mcp(cluster = "Tukey")))
cld_letters <- data.frame(cluster = names(letters$mcletters$Letters),
letters = letters$mcletters$Letters)
f_Theft <-
ggplot(crime_KM4, aes(x = cluster, y = Theft)) +
geom_boxplot() +
geom_text(data = cld_letters, aes(label = letters, x = c(1:4), y = max(crime_KM4$Theft)* 1.2)) +
ylim(0, max(crime_KM4$Theft) * 1.2) +
theme_classic()
#
aov_Vehicle <- aov(Vehicle ~ cluster, data = crime_KM4)
summary(aov_Vehicle) Df Sum Sq Mean Sq F value Pr(>F)
cluster 3 1427939 475980 30.08 6.46e-11 ***
Residuals 46 727932 15825
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1letters <- cld(glht(aov_Vehicle, linfct = mcp(cluster = "Tukey")))
cld_letters <- data.frame(cluster = names(letters$mcletters$Letters),
letters = letters$mcletters$Letters)
f_Vehicle <-
ggplot(crime_KM4, aes(x = cluster, y = Vehicle)) +
geom_boxplot() +
geom_text(data = cld_letters, aes(label = letters, x = c(1:4), y = max(crime_KM4$Vehicle) * 1.2)) +
ylim(0, max(crime_KM4$Vehicle) * 1.2) +
theme_classic()
library(patchwork)
f_Murder + f_Rape + f_Robbery +
f_Ausault + f_Burglary + f_Theft +
f_Vehicle +
plot_layout(ncol = 3, nrow = 3)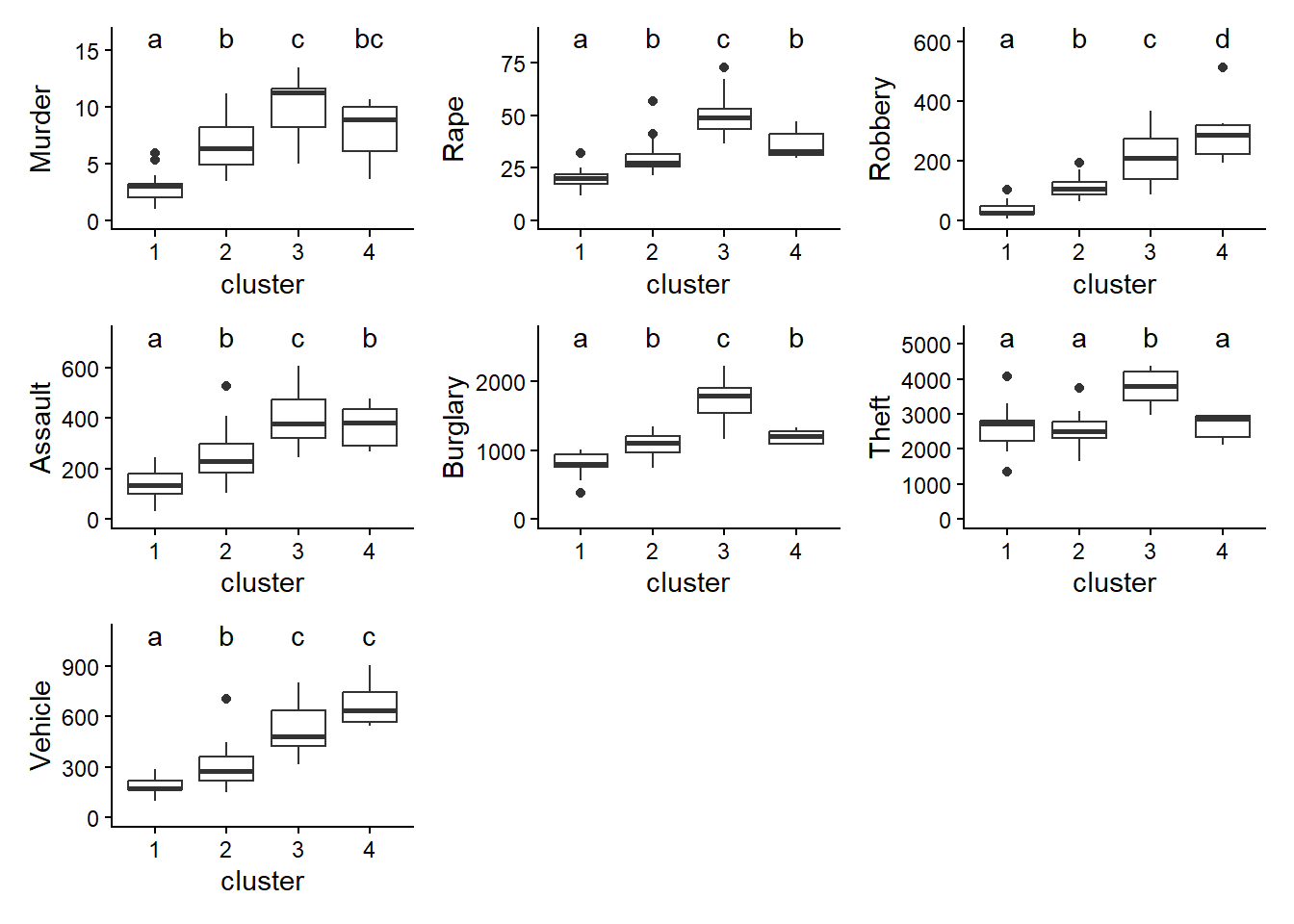
Die Boxplots erlauben jetzt auch eine Beurteilung der Modelldiagnostik: Die Residuen sind hinreichend normalverteilt (symmetrisch)
