Prepro 3: Übung

Aufgabe 1

Gegeben sei ein Datensatz sensors_combined.csv mit den Temperaturwerten von drei verschiedenen Sensoren. Importiere ihn als csv in R (als sensors_combined).

Formatiere die Datetime Spalte in POSIXct um. Verwende dazu die Funktion as.POSIXct (lies mit ?strftime() nochmal nach, wie du das spezifische Format (die “Schablone”) festlegen kannst).

library("readr")

sensors_combined <- read_delim("datasets/prepro/sensors_combined.csv", ",")

sensors_combined$Datetime <- as.POSIXct(sensors_combined$Datetime, format = "%d%m%Y_%H%M")

Aufgabe 2

Überführe die Tabelle in ein langes Format (verwende dazu die Funktion pivot_longer aus tidyr) und speichere den output als sensors_long.

Tipp:

• im Argument cols kannst du entweder die Spalten auflisten, die “pivotiert” werden sollen.
• Alternativ kannst du (mit vorangestelltem Minuszeichen, -) die Spalte bezeichnen, die nicht pivotiert werden soll.
• In beiden Fällen musst du die Spalten weder mit Anführungs- und Schlusszeichen noch mit dem $-Zeichen versehen.

library("tidyr")

# Variante 1 (Spalten abwählen)
sensors_long <- pivot_longer(sensors_combined, -Datetime) 

# Variante 2 (Spalten anwählen)
sensors_long <- pivot_longer(sensors_combined, c(sensor1:sensor3))

Aufgabe 3

Gruppiere sensors_long nach der neuen Spalte, wo die Sensor-Information enthalten ist (default: name) mit group_by und berechne den Mittelwert der Temperatur pro Sensor (summarise). Hinweis: Beide Funktionen sind Teil des Packages dplyr.

Der Output sieht folgendermassen aus:

library("dplyr")

sensors_long |>
  group_by(name) |>
  summarise(temp_mean = mean(value, na.rm = TRUE))
## # A tibble: 3 × 2
##   name    temp_mean
##   <chr>       <dbl>
## 1 sensor1      14.7
## 2 sensor2      12.0
## 3 sensor3      14.4

Aufgabe 4

Erstelle für sensors_long eine neue convenience Variabel month, welche den Monat beinhaltet (Tipp: verwende dazu die Funktion month aus lubridate). Gruppiere nun nach month und Sensor und berechne den Mittelwert der Temperatur.

library("lubridate")

sensors_long |>
  mutate(month = month(Datetime)) |>
  group_by(month, name) |>
  summarise(temp_mean = mean(value, na.rm = TRUE))

Aufgabe 5

Importiere die Datei sensor_fail.csv in R.

sensor_fail.csv hat eine Variabel SensorStatus: 1 bedeutet der Sensor misst, 0 bedeutet der Sensor misst nicht. Fälschlicherweise wurde auch dann der Messwert Temp = 0 erfasst, wenn Sensorstatus = 0. Richtig wäre hier NA (not available). Korrigiere den Datensatz entsprechend.

sensor_fail <- read_delim("datasets/prepro/sensor_fail.csv")

# mit base-R:
sensor_fail$Temp_correct[sensor_fail$SensorStatus == 0] <- NA
sensor_fail$Temp_correct[sensor_fail$SensorStatus != 0] <- sensor_fail$Temp #Warnmeldung kann ignoriert werden.

# das gleiche mit dplyr:
sensor_fail <- sensor_fail |>
  mutate(Temp_correct = ifelse(SensorStatus == 0, NA, Temp))

Sensor	Temp	Hum_%	Datetime	SensorStatus	Temp_correct
Sen102	0.6	98	16102017_1800	1	0.6
Sen102	0.3	96	17102017_1800	1	0.3
Sen102	0.0	87	18102017_1800	1	0.0
Sen102	0.0	86	19102017_1800	0	NA
Sen102	0.0	98	23102017_1800	0	NA
Sen102	0.0	98	24102017_1800	0	NA
Sen102	0.0	96	25102017_1800	1	0.0
Sen103	-0.3	87	26102017_1800	1	-0.3
Sen103	-0.7	98	27102017_1800	1	-0.7
Sen103	-1.2	98	28102017_1800	1	-1.2

Aufgabe 6

Warum spielt es eine Rolle, ob 0 oder NA erfasst wird? Berechne den Mittelwert der Temperatur / Feuchtigkeit nach der Korrektur.

# Mittelwerte der falschen Sensordaten: 0 fliesst in die Berechnung
# ein und verfälscht den Mittelwert
mean(sensor_fail$Temp)

# Mittelwerte der korrigierten Sensordaten: mit na.rm = TRUE werden
# NA-Werte aus der Berechnung entfernt.
mean(sensor_fail$Temp_correct, na.rm = TRUE)

Aufgabe 7

Lade jetzt nochmal den Datensatz weather.csv (Quelle MeteoSchweiz) herunter und importiere ihn als CSV mit den korrekten Spaltentypen (stn als factor, time als POSIXct, tre200h0 als double).

weather <- read_delim("datasets/prepro/weather.csv")

weather$stn <- as.factor(weather$stn)

weather$time <- as.POSIXct(as.character(weather$time), format = "%Y%m%d%H")

Aufgabe 8

Erstelle nun eine convenience Variable für die Kalenderwoche pro Messung (lubridate::week). Berechne im Anschluss den Mittelwert der Temperatur pro Kalenderwoche.

weather_summary <- weather |>
  mutate(week = week(time)) |>
  group_by(week) |>
  summarise(
    temp_mean = mean(tre200h0, na.rm = TRUE)
  )

Visualisiere im Anschluss das Resultat:

plot(weather_summary$week, weather_summary$temp_mean, type = "l")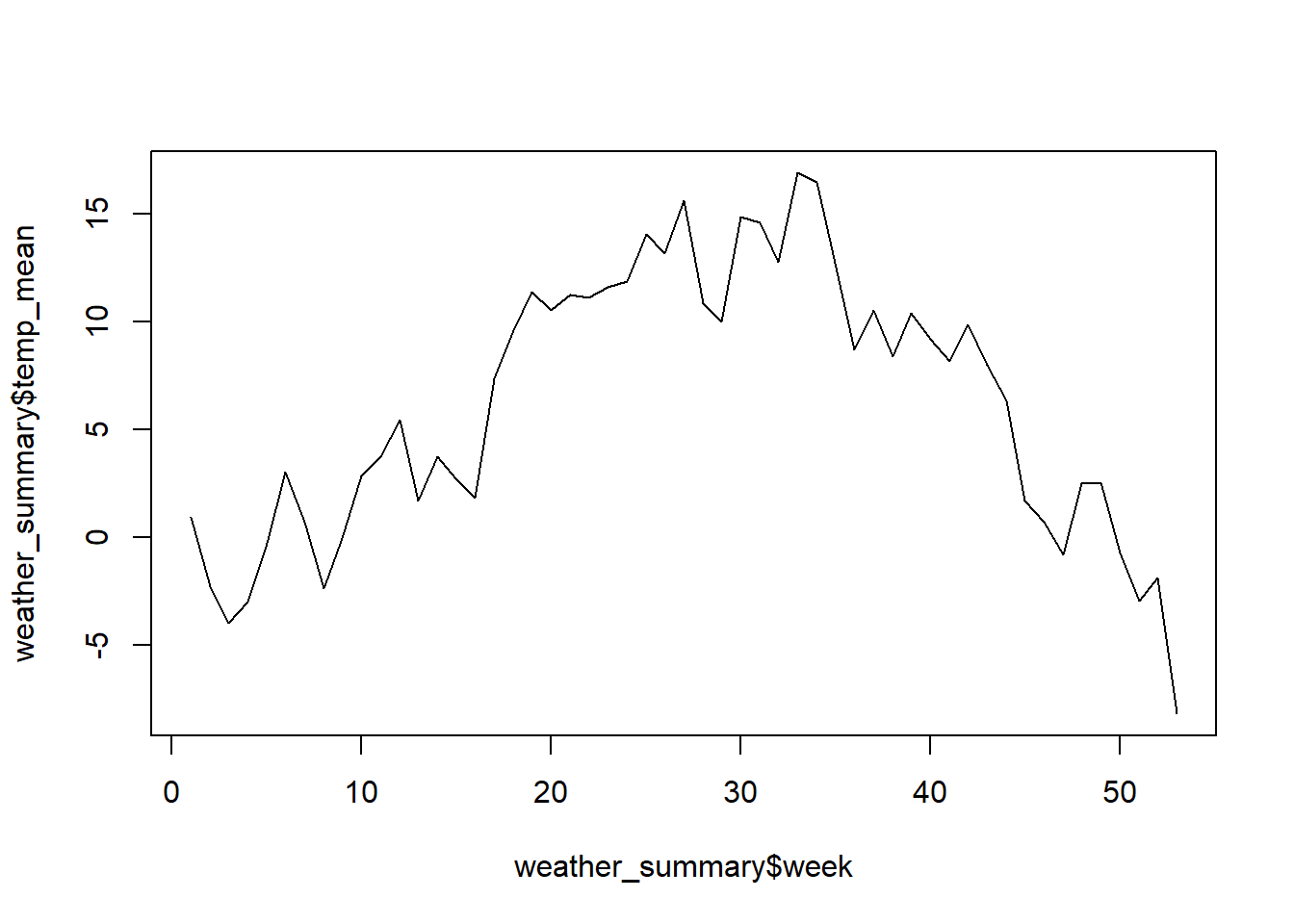

Aufgabe 9

In der vorherigen Aufgabe haben wir den Mittelwert der Temperatur pro Kalenderwoche über alle Jahre (2000 und 2001) berechnet. Wenn wir die Jahre aber miteinander vergleichen wollen, müssen wir das Jahr als zusätzliche convenience Variable erstellen und danach gruppieren. Versuche dies mit den Wetterdaten und visualisiere den Output anschliessend.

weather_summary2 <- weather |>
  mutate(
    week = week(time),
    year = year(time)
    ) |>
  group_by(year, week) |>
  summarise(
    temp_mean = mean(tre200h0, na.rm = TRUE)
  )

plot(weather_summary2$week, weather_summary2$temp_mean, type = "l")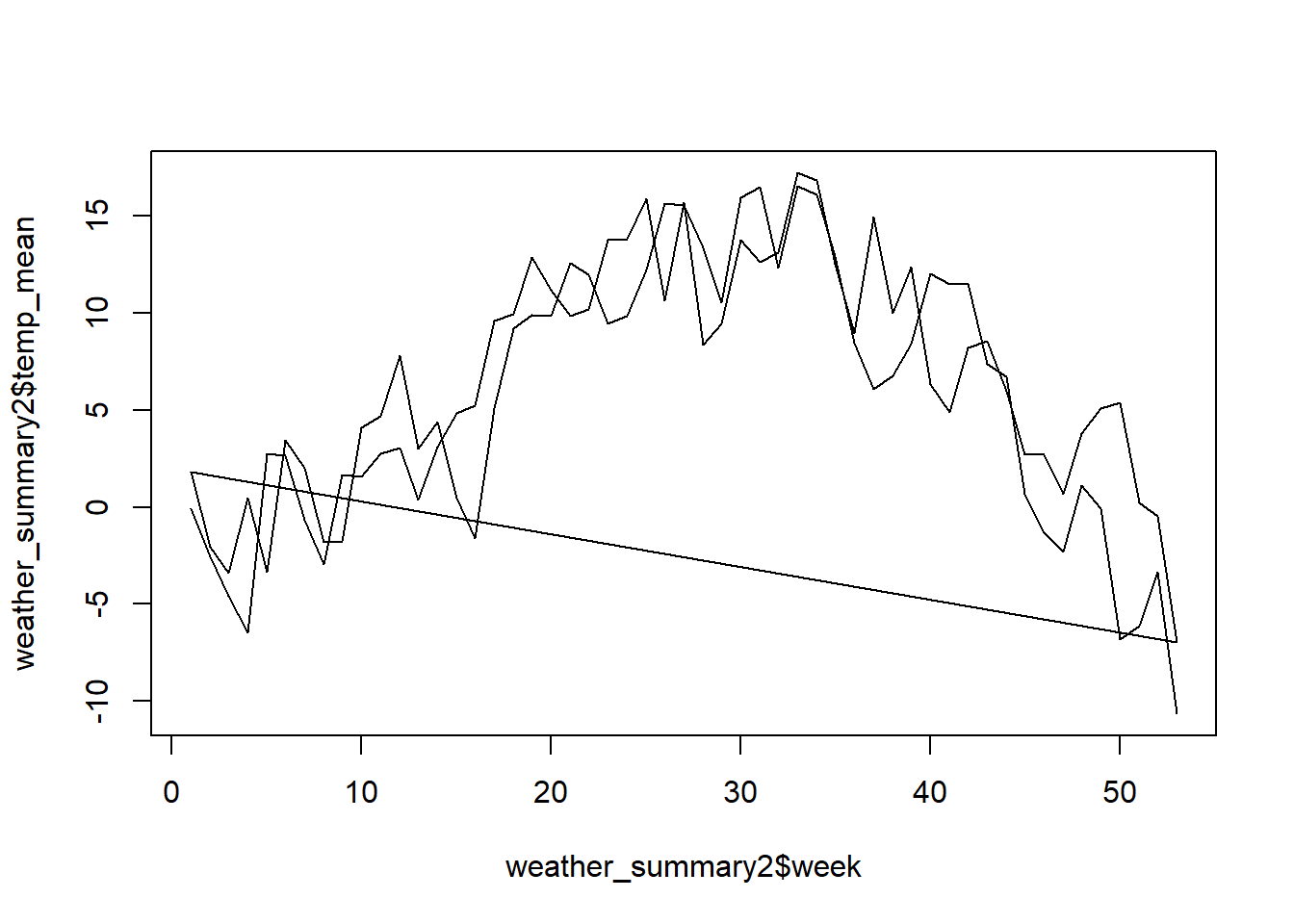

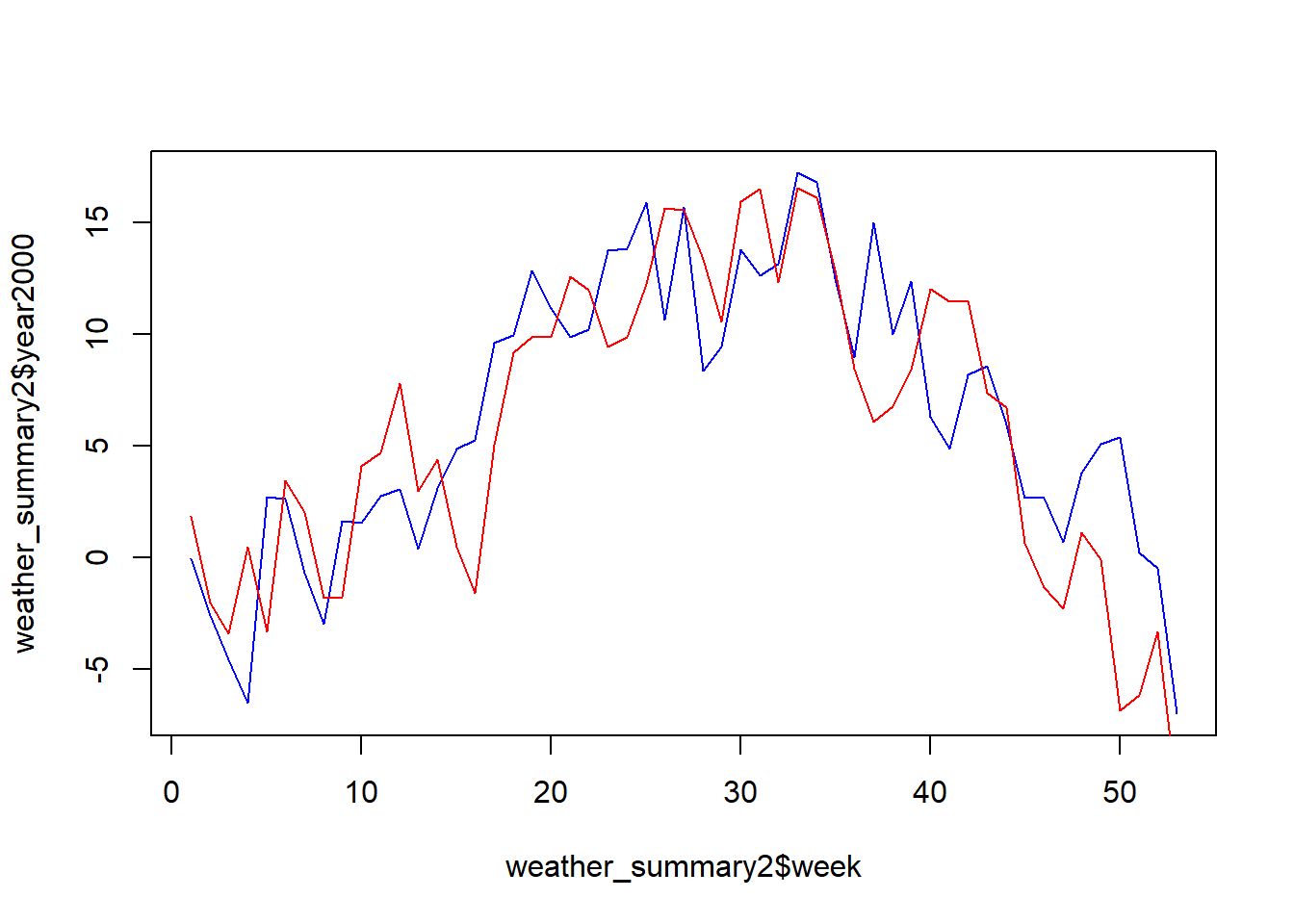
Abbildung 7.1: baseplot mag keine long tables und macht aus den beiden Jahren eine kontinuierliche Linie

Aufgabe 10

Überführe den Output aus der letzten Übung in eine wide table. Nun lassen sich die beiden Jahre viel besser miteinander vergleichen.

weather_summary2 <- weather_summary2 |>
  pivot_wider(names_from = year, values_from = temp_mean,names_prefix = "year")

plot(weather_summary2$week, weather_summary2$year2000, type = "l",col = "blue")
lines(weather_summary2$week, weather_summary2$year2001, type = "l",col = "red")