Einstieg Multivariate Modelle / Habitatselektionsmodell

Libraries laden

library("sf")
library("terra")
library("dplyr")
library("readr")
library("ggplot2")
library("PerformanceAnalytics")
library("pastecs")
library("car")
library("psych")
library("DHARMa")

options(scipen = 999)

Aufgabe 1

Einlesen der Gesamtdatensätze für die Multivariate Analysen von Moodle

  1. Sichtung der Datensätze, der Variablen und der Datentypen
  2. Kontrolle wieviele Rehe/Rothirsche in den Datensätzen enthalten sind
Musterlösung 
DF_reh <- read_delim("datasets/fallstudie_n/Aufgabe_4/Aufgabe4_Datensatz_Modelle_Habitatnutzung_Reh_251027.csv", delim = ";")

str(DF_reh)

class(DF_reh$time_of_day)

table(DF_reh$id)

DF_reh |>
  group_by(id) |>
  summarize(anzahl = n())

length(unique(DF_reh$id))

Aufgabe 2

Unterteilung des Datensatzes in Teildatensätze entsprechend der Tageszeit

Musterlösung 
DF_reh_night <- DF_reh |>
  filter(time_of_day == "night")

DF_reh_day <- DF_reh |>
  filter(time_of_day == "day")

Aufgabe 3

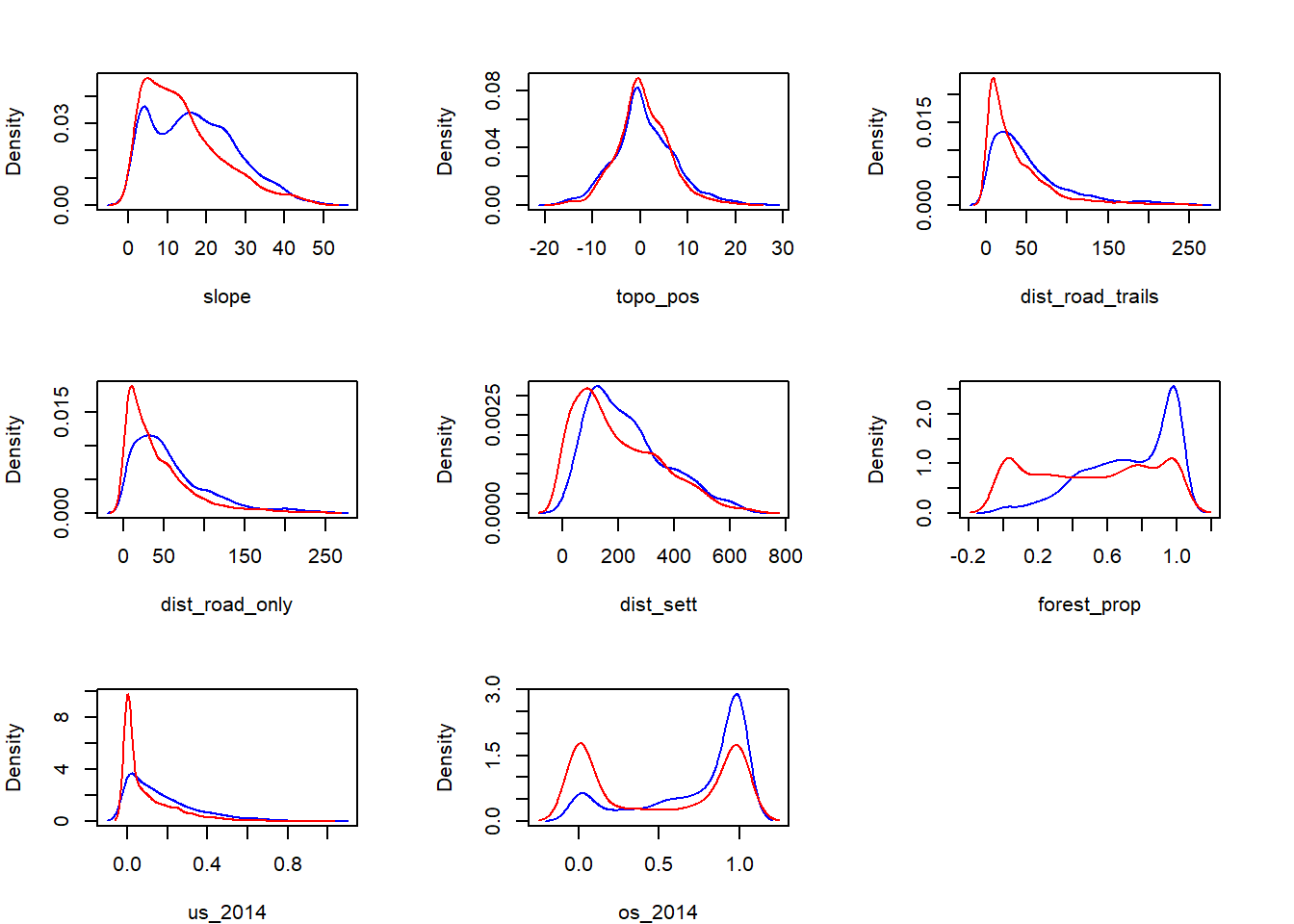
Erstellen von Density Plots der Präsenz / Absenz in Abhängigkeit der unabhängigen Variablen. Diese Übung dient einer ersten groben Einschätzung der Wirkung der Umweltvariablen auf die abhängige Variable (Präsenz/Absenz in unserem Fall)

# Ein Satz Density Plots für den Tagesdatensatz und einer für den Nachtdatensatz

par(mfrow = c(3, 3), mar = c(4, 4, 3, 3)) # Vorbereitung Raster für Plots

# innerhalb des for()-loops die Nummern der gewünschten Spalten einstellen

for (i in 5:12) {
  dp <- DF_reh_day |> filter(pres_abs == 1) |> pull(i)
  dp <- density(dp)
  da <- DF_reh_day |> filter(pres_abs == 0) |> pull(i)
  da <- density(da)
  plot(0, 0, type = "l",
    xlim = range(c(dp$x, da$x)),
    ylim = range(dp$y, da$y),
    xlab = names(DF_reh_day[i]),
    ylab = "Density"
  )
  lines(dp$x, dp$y, col = "blue")             # Präsenz = used
  lines(da$x, da$y, col = "red")              # Absenz = available
}

Aufgabe 4

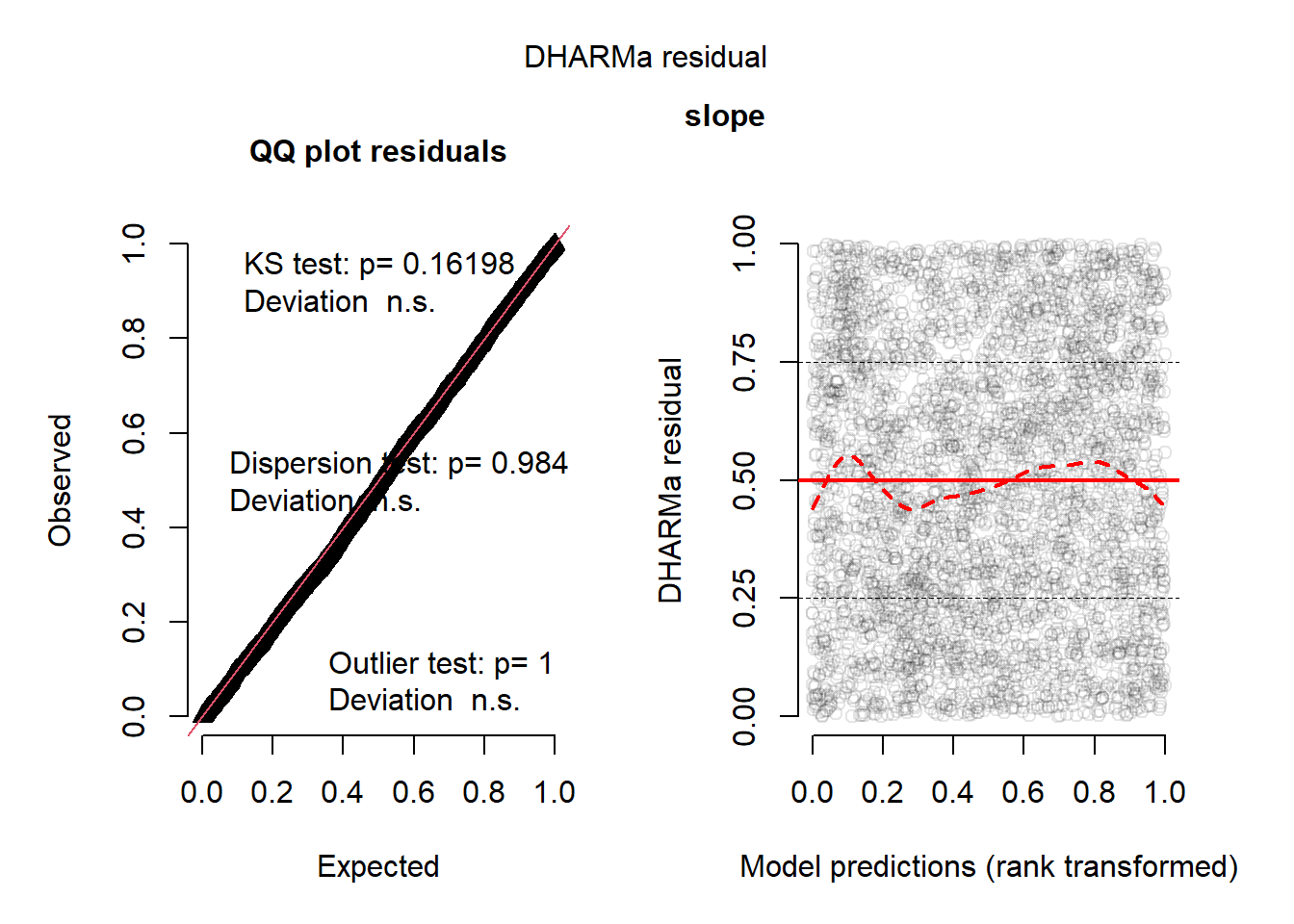
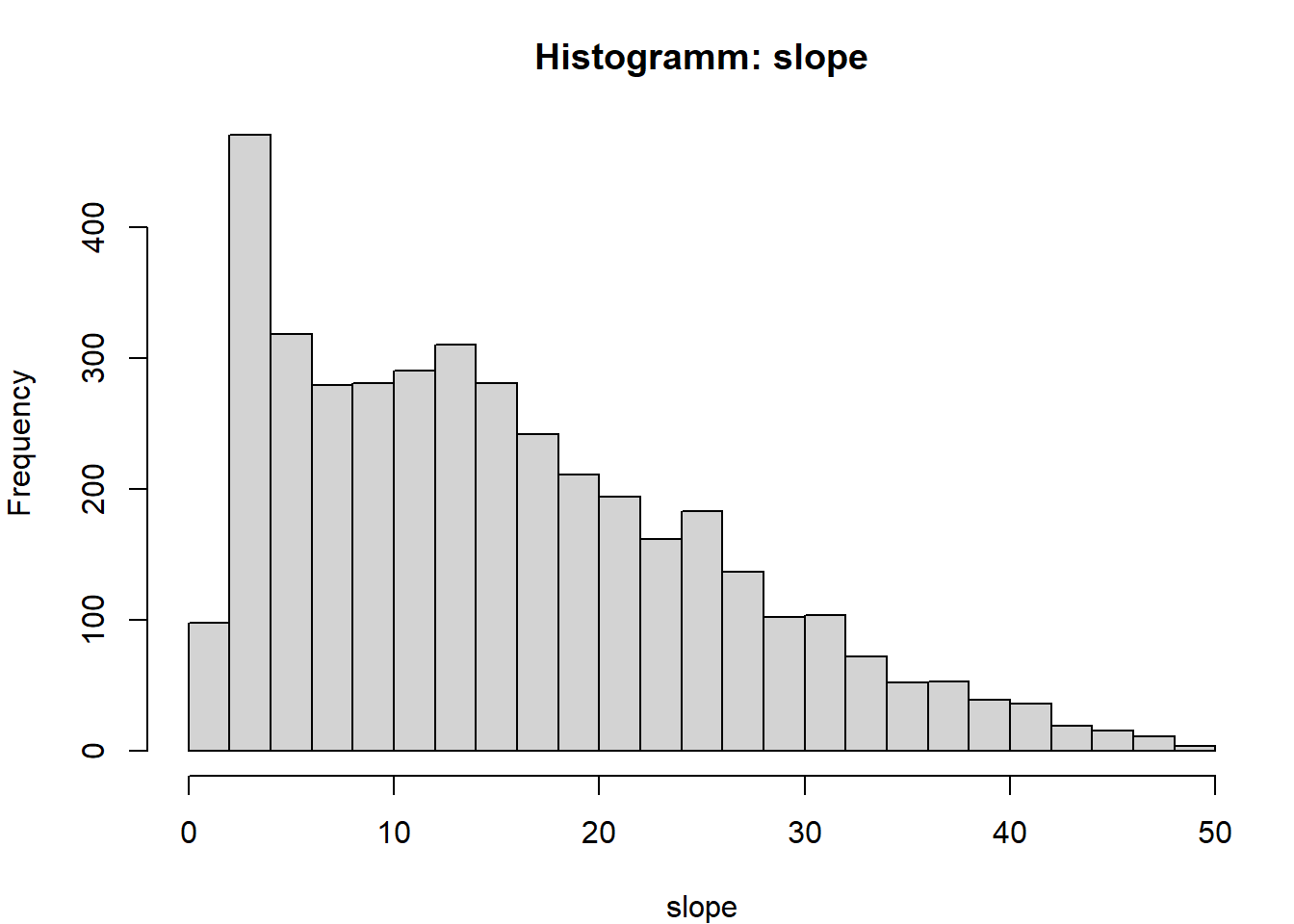
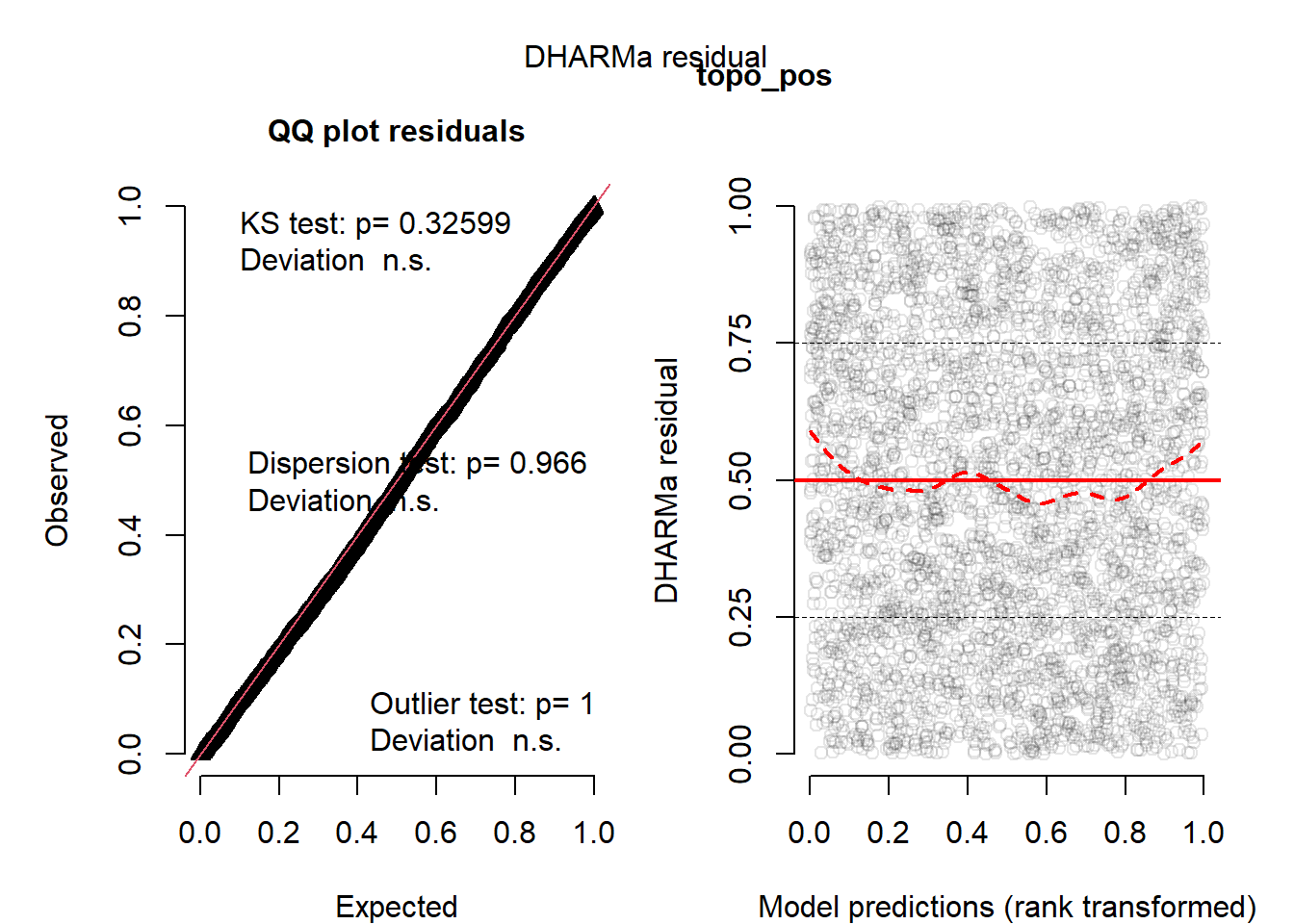
Für jede kontinuierliche Variable: ein binomiales GLM fitten (pres_abs ~ x, data = DF_mod_day, family = binomial), Residuen berechnen und ein Histogramm + Q-Q-Plot (Residuen sollen grob „normal“ wirken) plotten. Wenn starke Abweichungen auftreten (krummes Histogramm, Q-Q-Punkte weit von der Linie): Transformationen probieren, das Modell neu fitten und die Residuen nochmal überprüfen.

Musterlösung 

# Definition des zu verarbeitenden Teildatensatzes 

data <- DF_reh_day

# Liste mit den zu verarbeitenden kontinuierlichen Variablen

vars <- c("slope","topo_pos","dist_road_trails","dist_road_only",
          "dist_sett","forest_prop","us_2014","os_2014")

# Ausgabe-Datei als PDF

out_pdf <- "fallstudie_n/glm_DHARMa_checks_DF_reh_day.pdf"

pdf(out_pdf, width = 7, height = 6)
on.exit(dev.off(), add = TRUE)

# Loop über die Variablen

for (v in vars) {
  if (!v %in% names(data)) next
  x <- data[[v]]
  if (sum(!is.na(x)) < 30 || length(unique(na.omit(x))) < 3) next

  # GLM fitten
  m   <- glm(as.formula(paste0("pres_abs ~ ", v)), data = data, family = binomial)

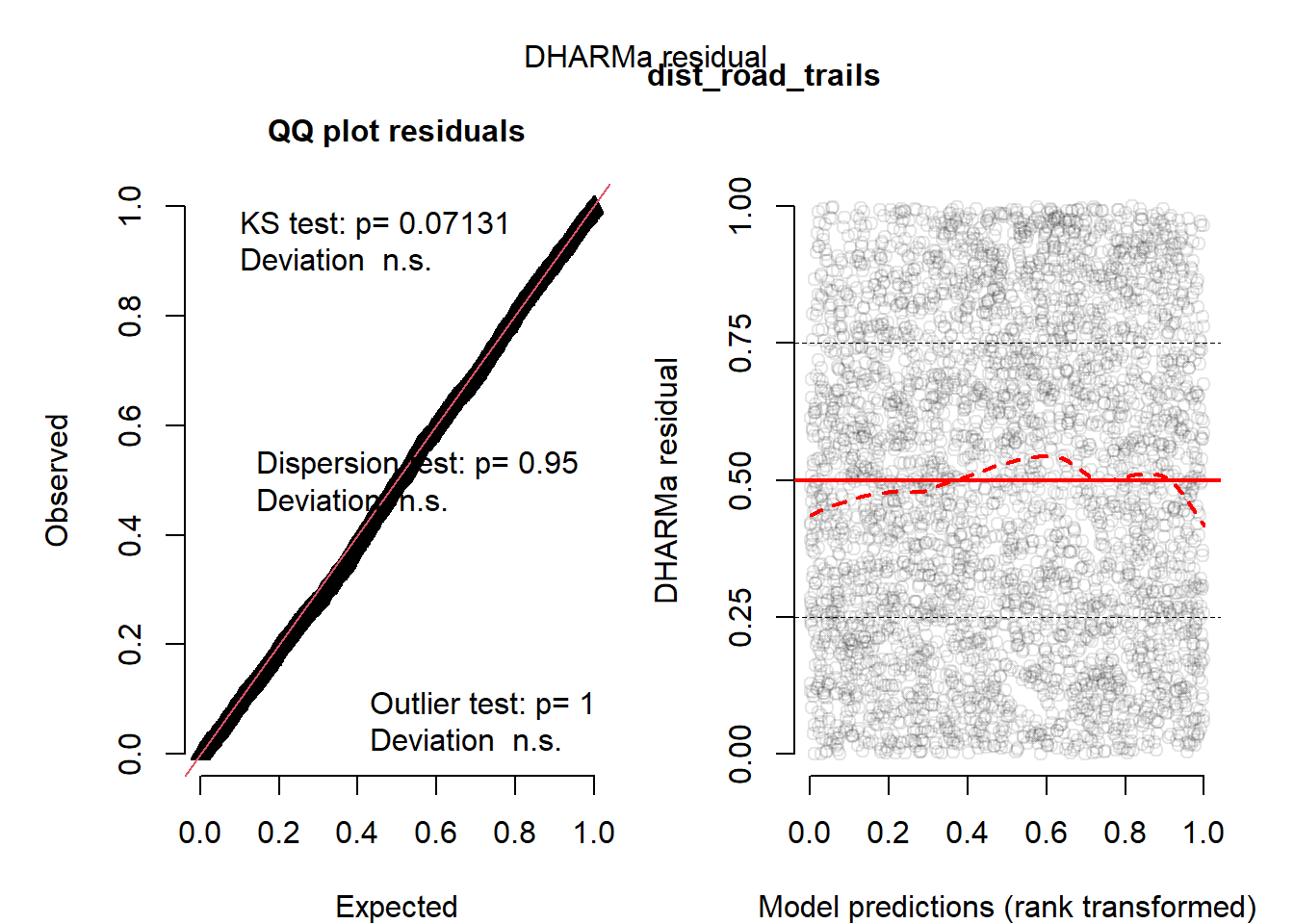
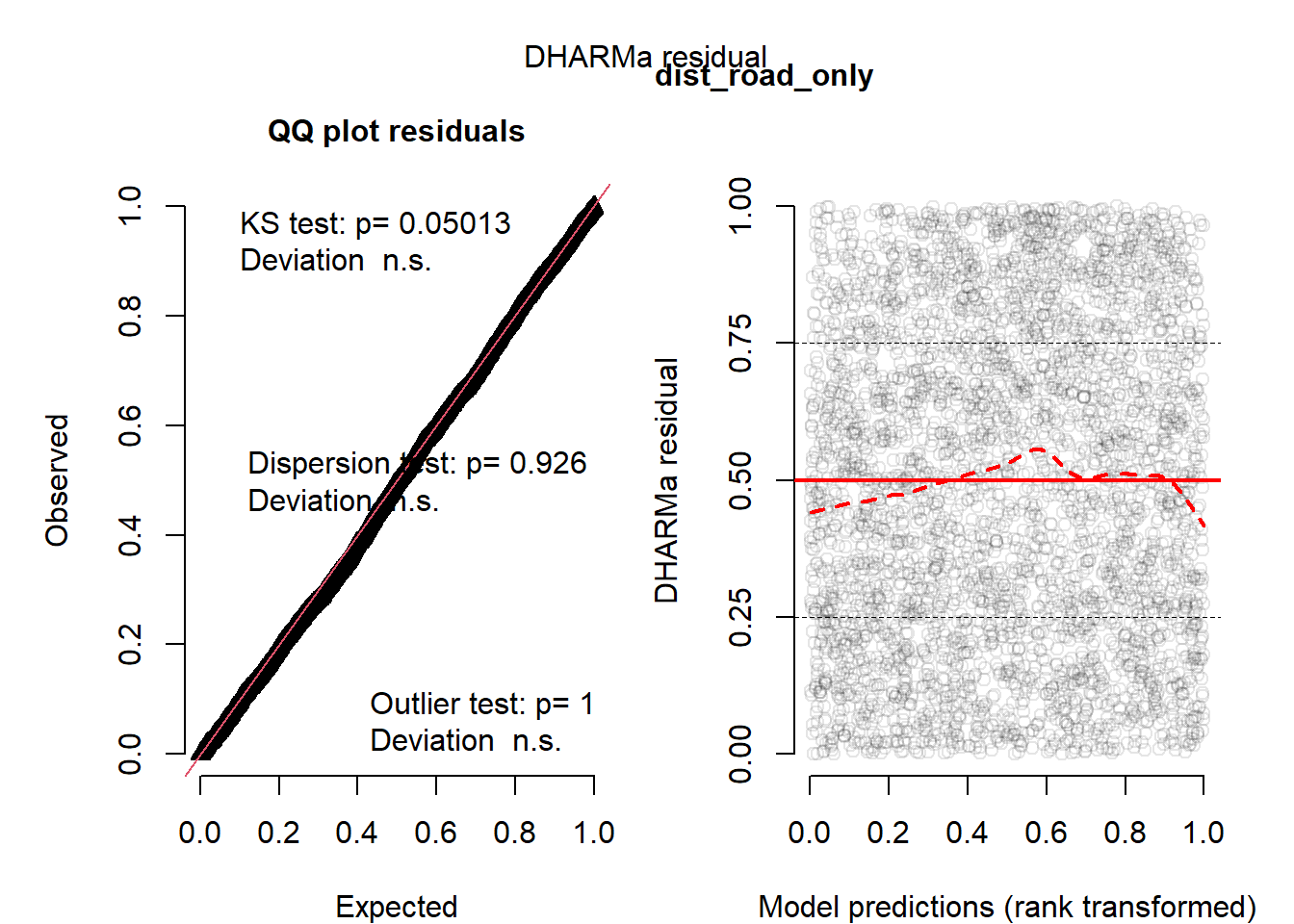
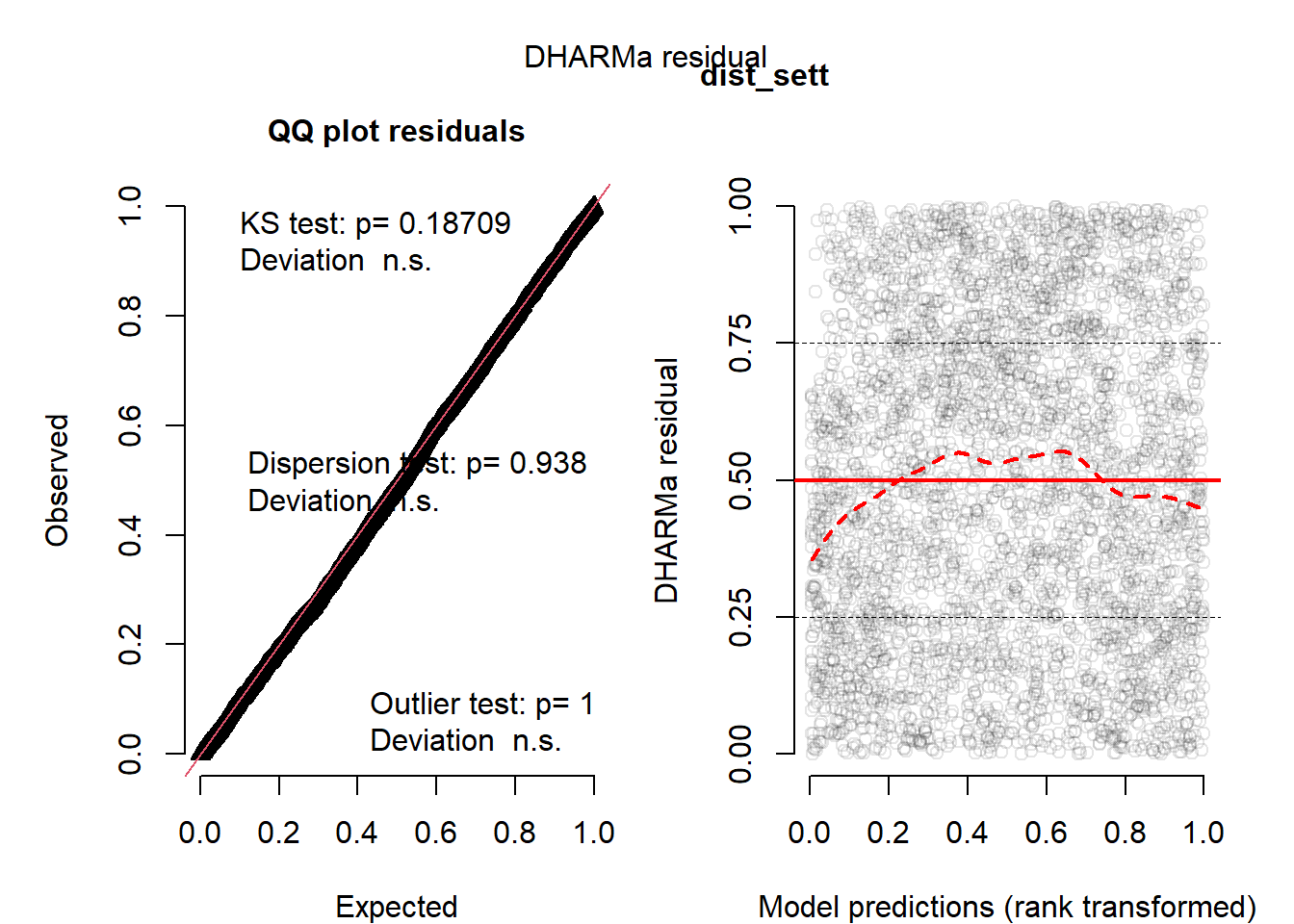
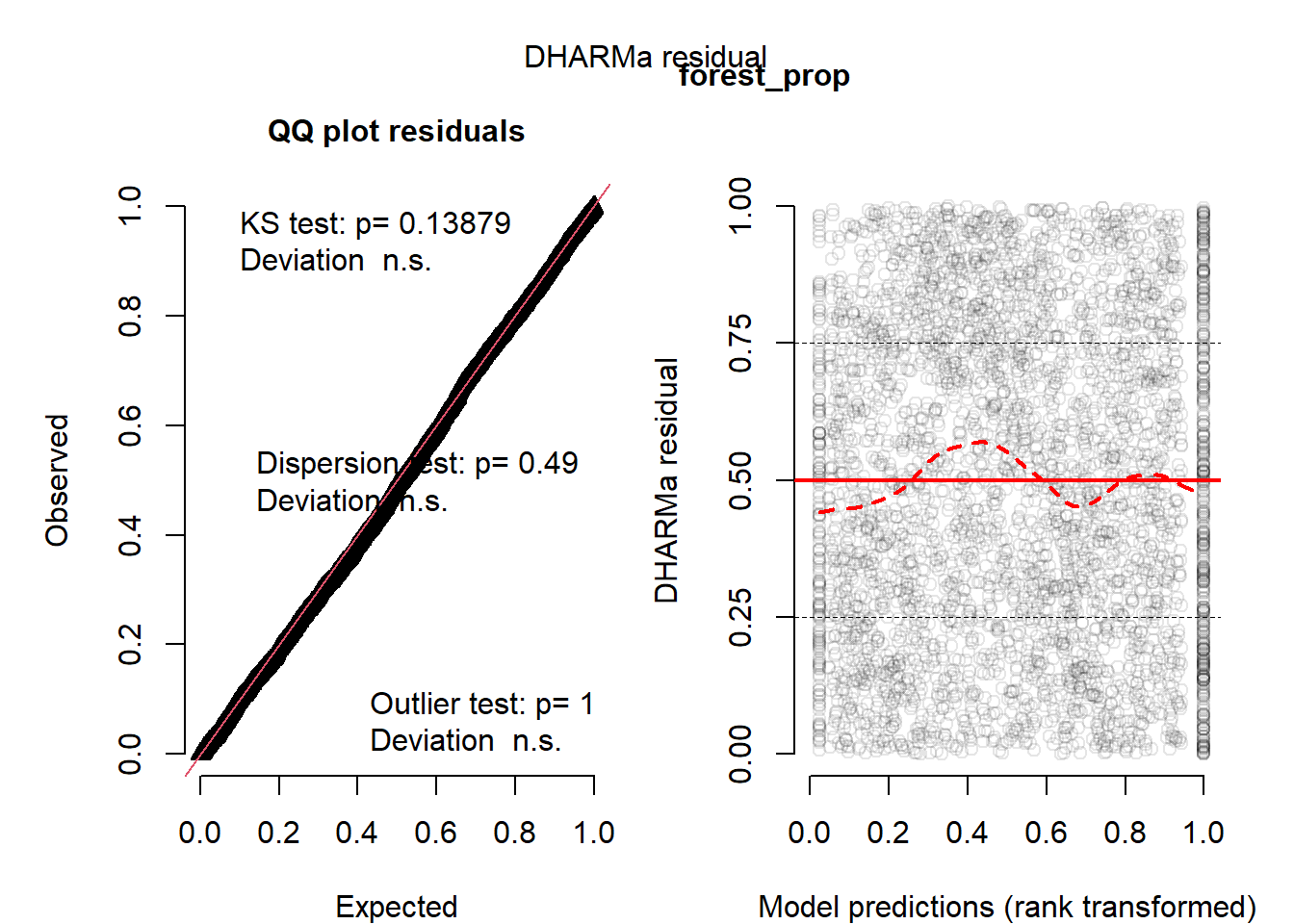
  # DHARMa Standardseite (QQ + Residuen vs Fitted)
  sim <- simulateResiduals(m, n = 1000, plot = FALSE)

  plot(sim, main = "")                 # Standardtitel ausblenden
  mtext(v, side = 3, line = 0.5, font = 2)  # eigene Überschrift (nur Variablenname)
  
  # Histogramm der Variable
  par(mfrow = c(1,1), mar = c(4,4,3,1))
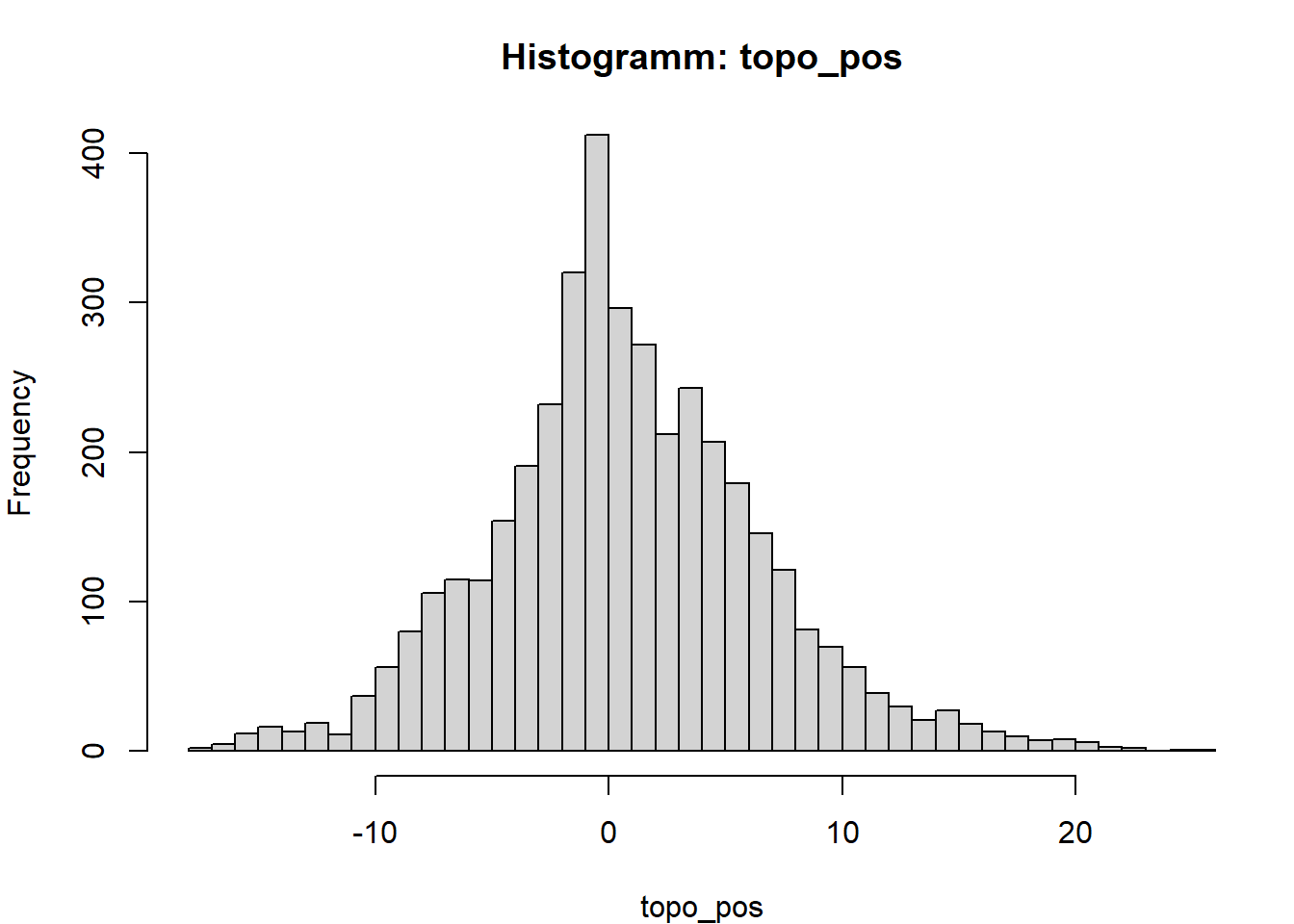
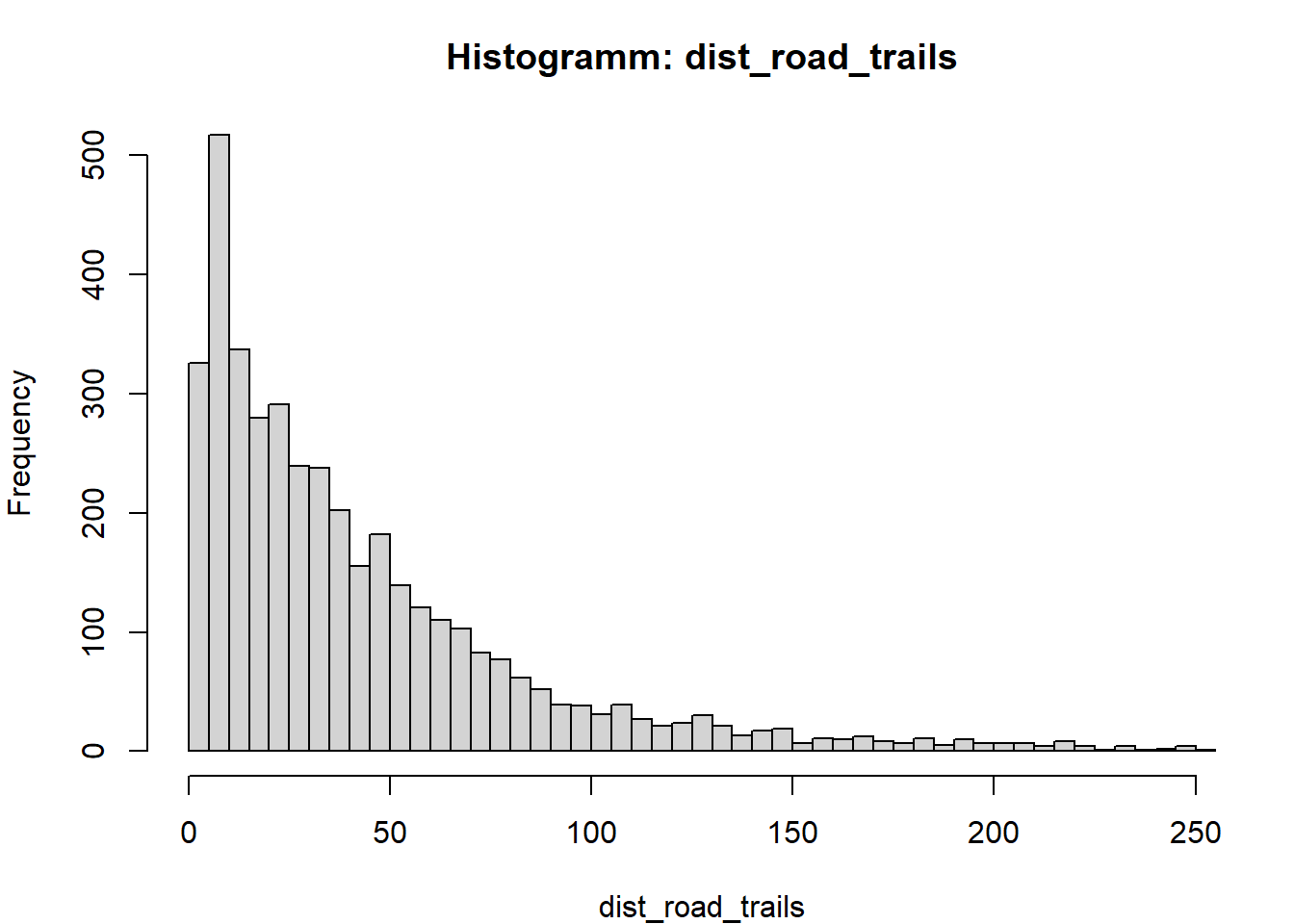
  hist(x, breaks = "FD", main = paste("Histogramm:", v), xlab = v)

}

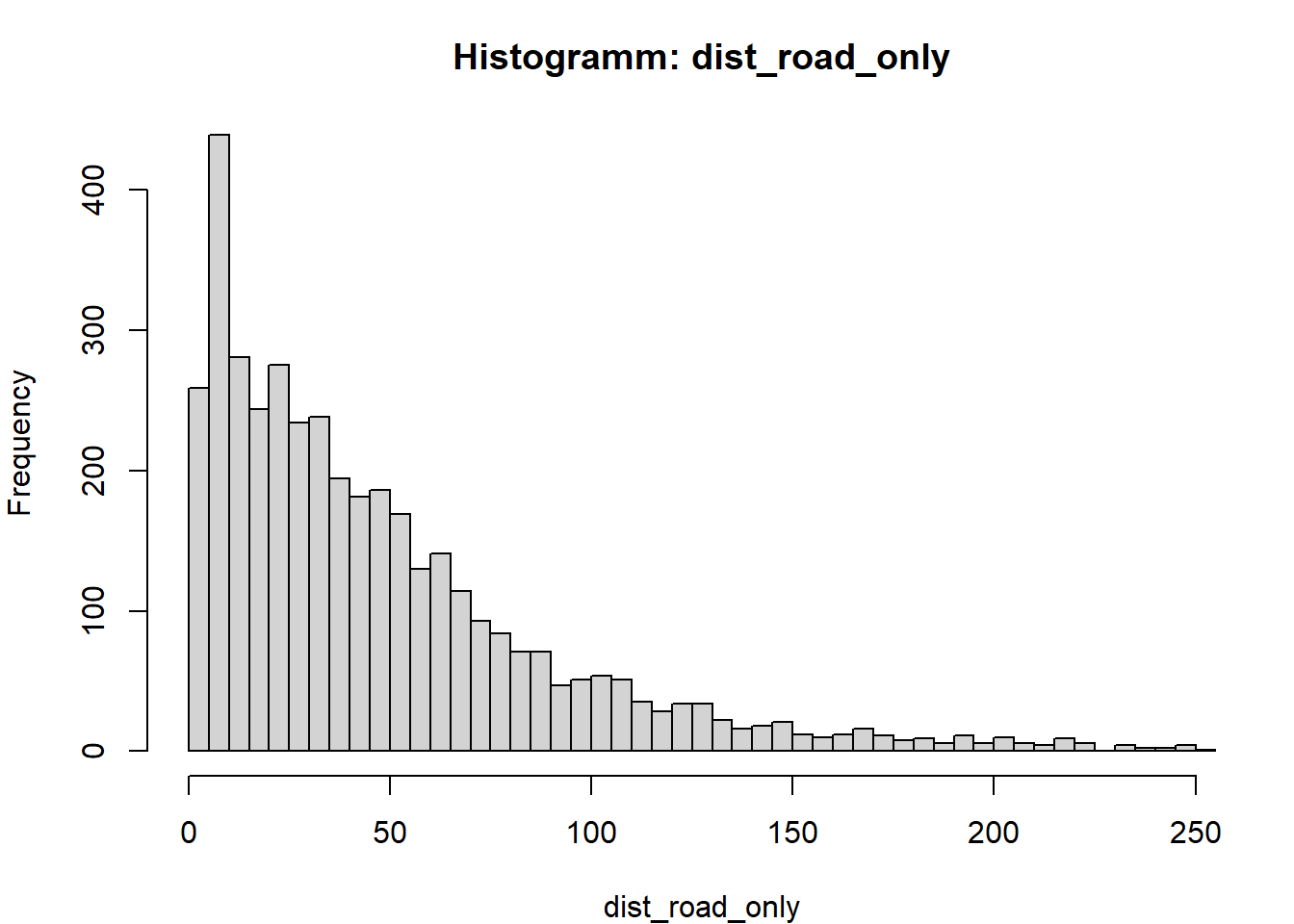
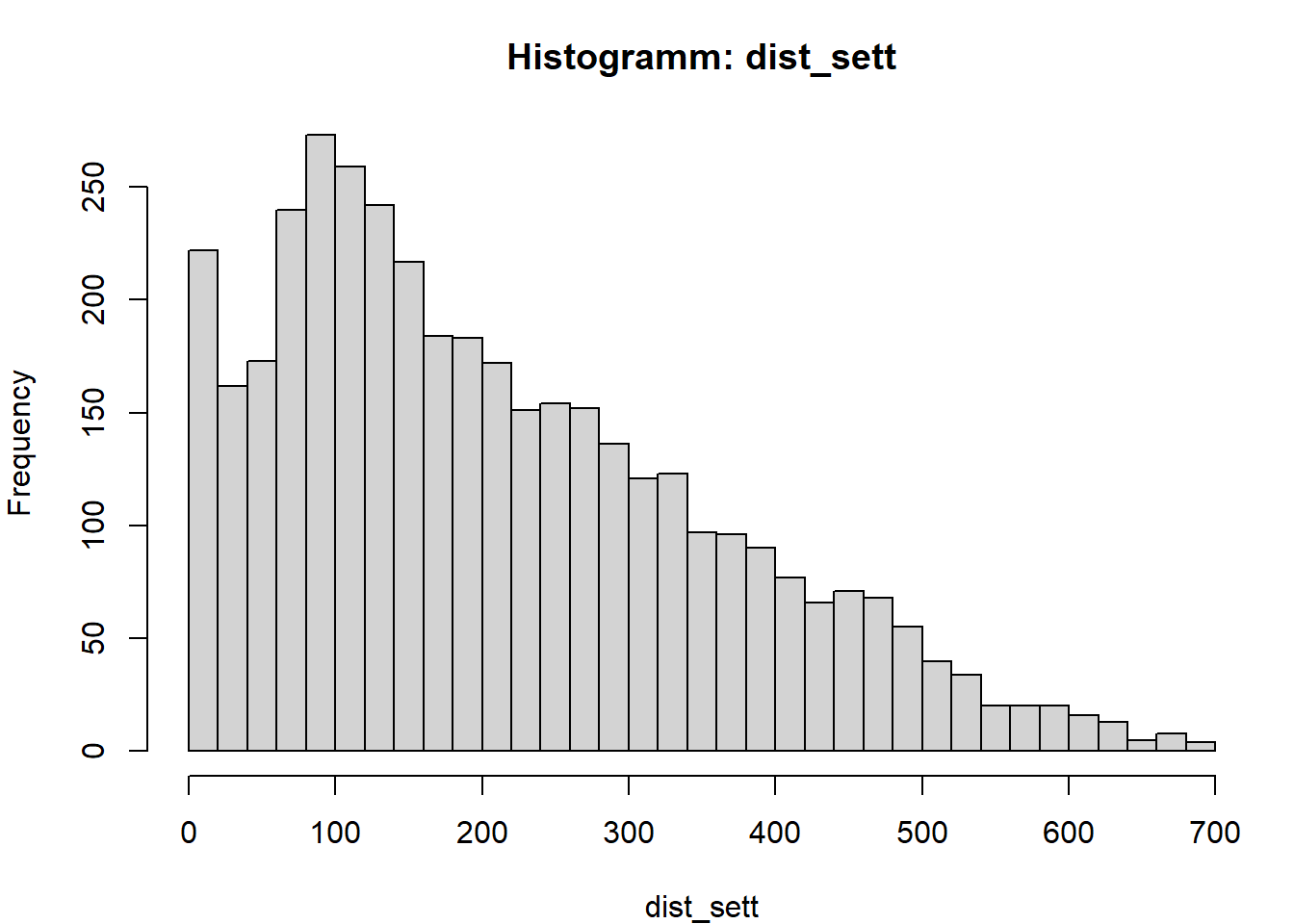
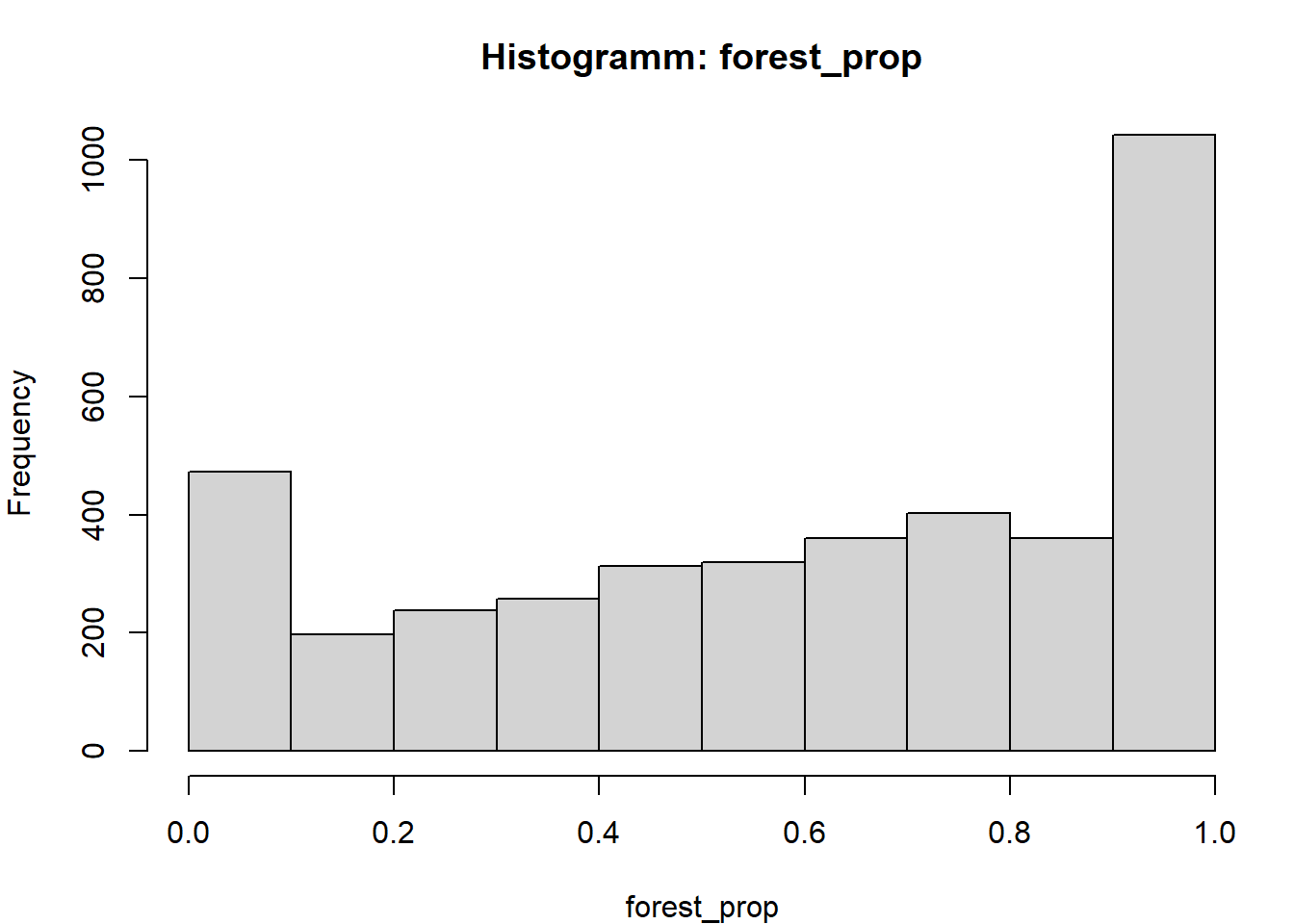
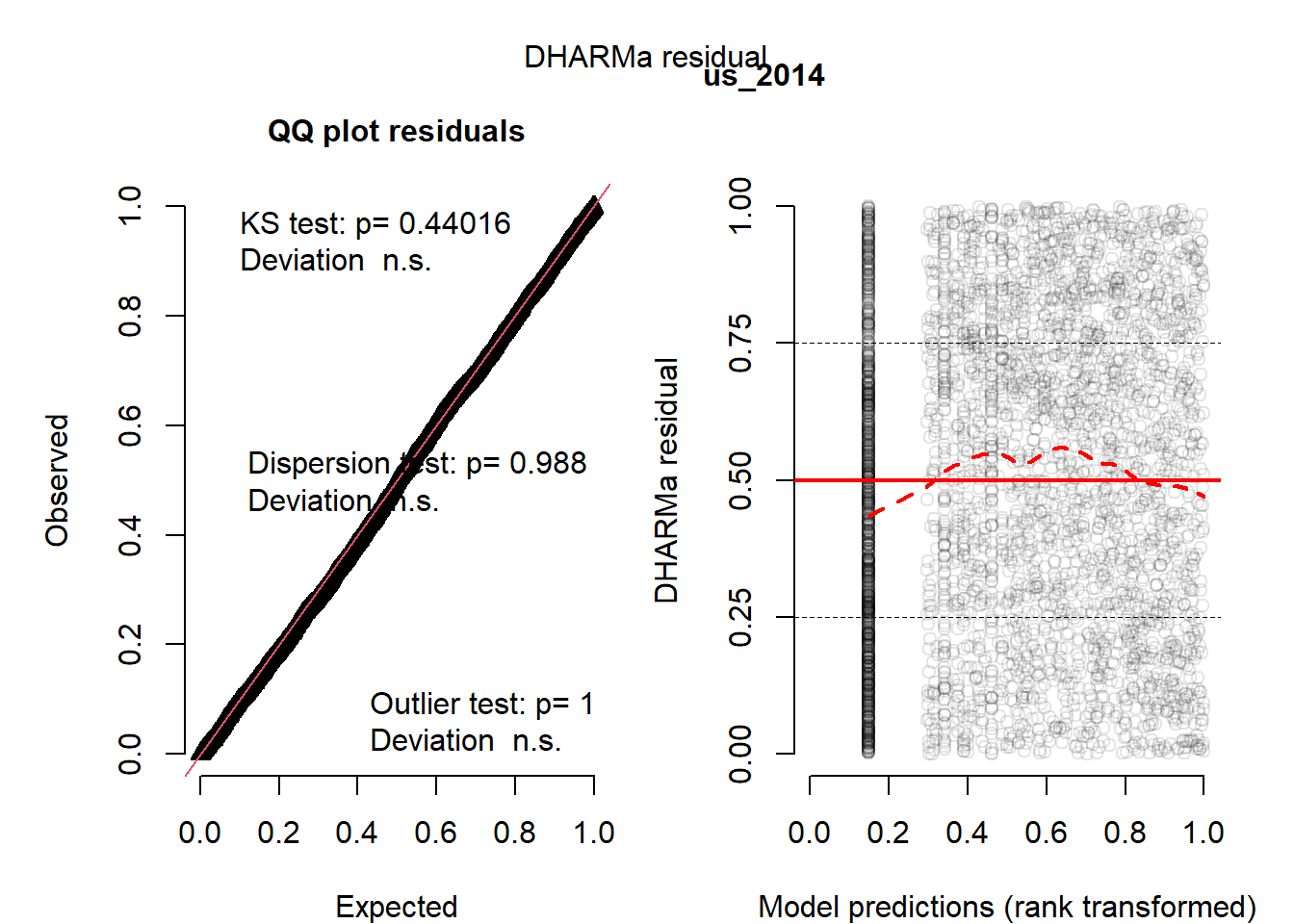
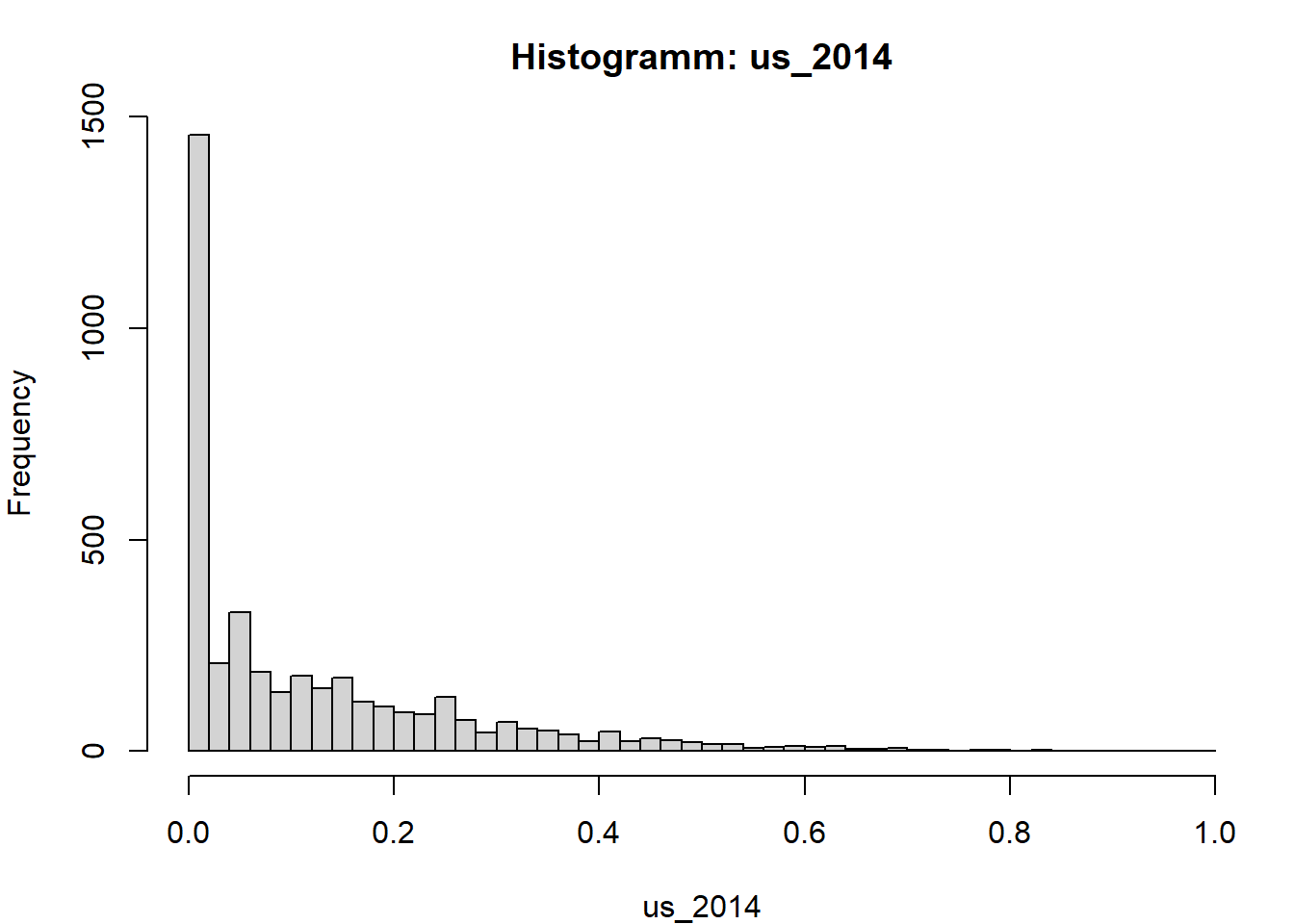
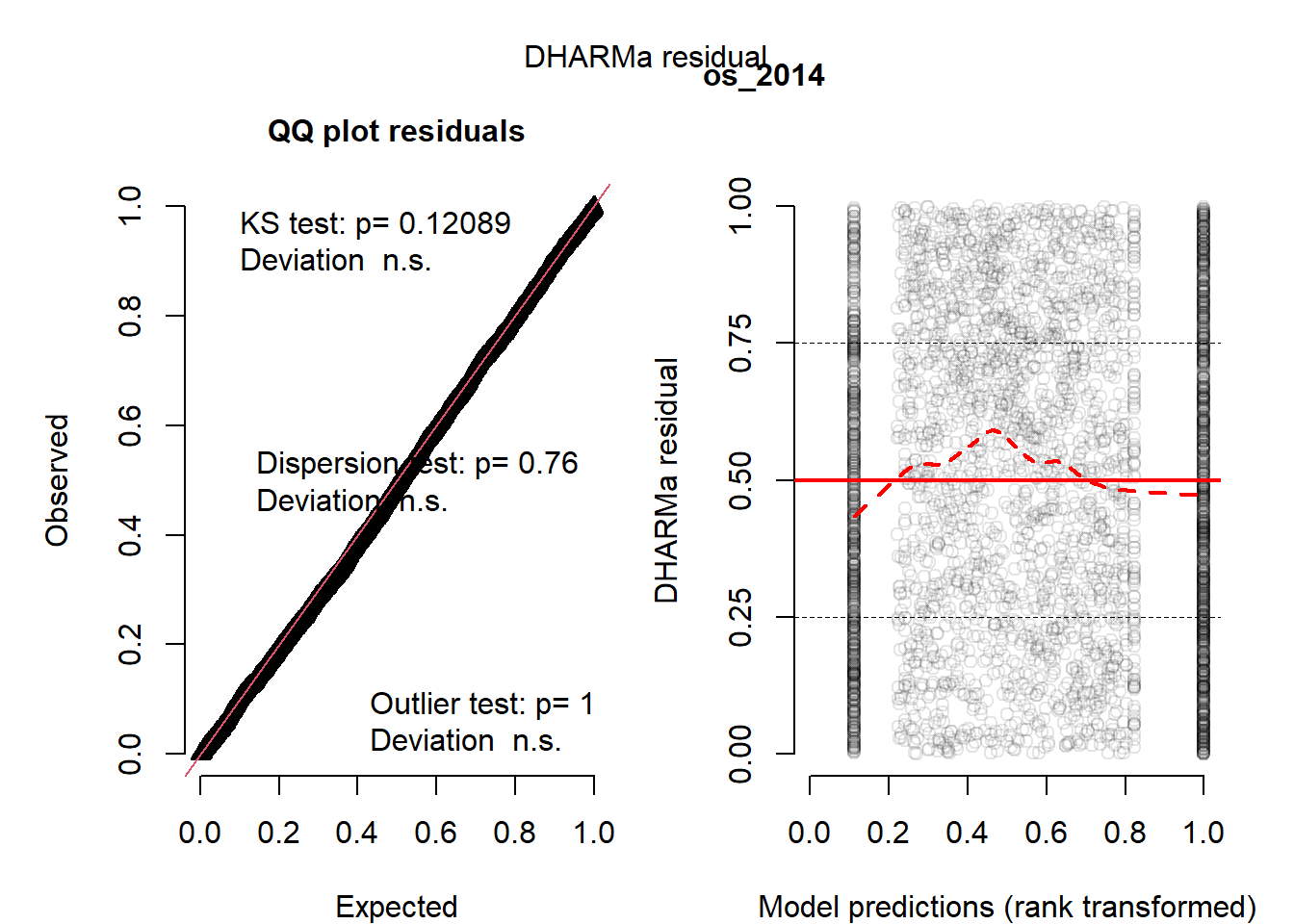
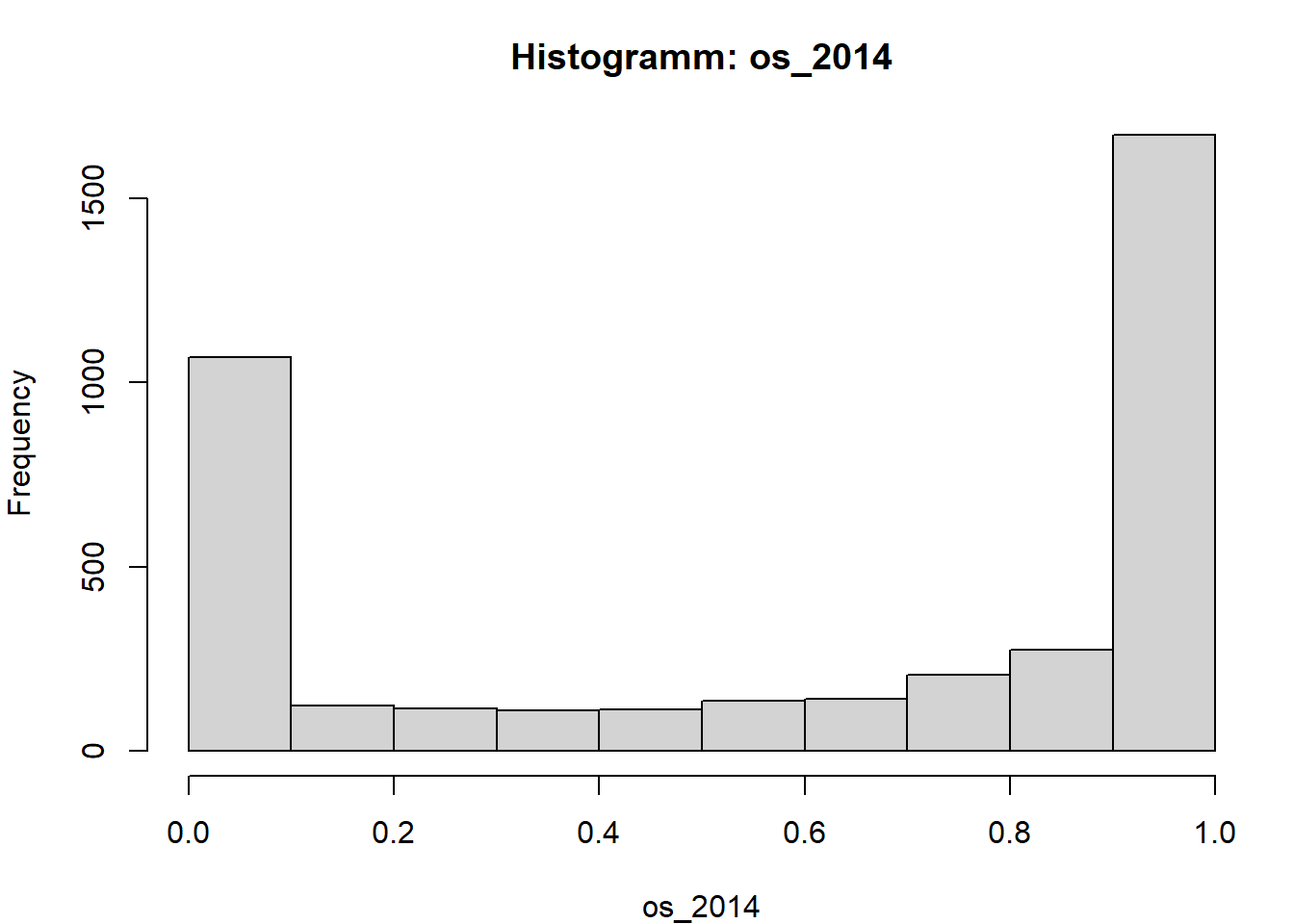
Aufgabe 5

Explorative Analysen der Variablen mit Scatterplots / Scatterplotmatrizen

  1. Zu Scatterplots und Scatterplotmatrizen gibt es viele verschiedene Funktionen / Packages, schaut im Internet und sucht euch eines welches euch passt.
  2. Testen der Korrelation zwischen den Variablen (Parametrisch oder nicht-parametrische Methode? Ausserdem: gewisse Scatterplotmatrizen zeigen euch die Koeffizenten direkt an)
Musterlösung 
pairs.panels(DF_reh_day[5:12],
  method = "pearson", # correlation method
  hist.col = "#00AFBB",
  density = TRUE, # show density plots
  ellipses = TRUE # show correlation ellipses
)

Musterlösung 

# Die Korrelation bei einem Teildatensatz zu testen reicht,
# denn die verwendeten Kreise sind die selben am Tag und in der Nacht,
# nur die Nutzung durch das Reh nicht.