library("sf")
library("dplyr")
library("ggplot2")
library("gstat")Rauman 3: Übung B
In dieser Übung geht es darum, zwei verschiedene Interpolationsverfahren in R umzusetzen. Im ersten Interpolationsverfahren verwenden wir die inverse distance weighted interpolation, später verwenden wir die nearest neighbour Methode. Dazu braucht ihr die folgenden Packages:
Weiter benötigt ihr die nachstehenden Datensätze:
- luftqualitaet.gpkg: Dieser Datensatz beinhaltet Messungen von Stickstoffdioxid \(NO_2\) aus dem Jahr 2015 für 97 Messstellen in der Schweiz. Stickstoffdioxid entsteht beim Verbrennen von Brenn- und Treibstoffen, insbesondere bei hohen Verbrennungstemperaturen, wobei der Strassenverkehr als Hauptquelle gilt. Mehr Informationen dazu findet ihr hier.
- schweiz.gpkg: Landesgrenze der Schweiz
Importiere diese in R. Prüfe, ob das CRS korrekt gesetzt wurde und setze es wenn nötig. Mache dich mit den Daten vertraut (visualieren, durchscrollen usw).
luftqualitaet <- read_sf("datasets/rauman/luftqualitaet.gpkg")
schweiz <- read_sf("datasets/rauman/schweiz.gpkg")Die Library gstat bietet verschiedene Möglichkeiten, Datenpunkte zu interpolieren, unter anderem auch die inverse distance weighted Methode. Leider ist das Package noch nicht so benutzerfreundlich wie sf: Das Package wird aber aktuell überarbeitet und in mittlerer Zukunft sollte es ebenso einfach zugänglich sein. Damit Ihr Euch nicht mit den Eigenheiten dieser Library herumschlagen müsst, haben wir eine Function vorbereitet, die Euch die Verwendung der IDW-Interpolation erleichtern soll.
Wir nehmen Euch damit etwas Komplexität weg und liefern Euch ein pfannenfertiges Werkzeug. Das hat auch Nachteile und wir ermutigen alle, die dafür Kapazität haben, unsere Funktion eingehend zu studieren und allenfalls ganz auf die Funktion zu verzichten und stattdessen direkt gstat zu verwenden. Wenn ihr mit unserer Funktion arbeiten möchtet, müsst ihr den unten stehenden Code in euer Skript kopieren und ausführen.
my_idw <- function(groundtruth, column, cellsize, nmax = Inf, maxdist = Inf, idp = 2, extent = NULL){
library("gstat")
library("sf")
if(is.null(extent)){
extent <- groundtruth
}
samples <- st_make_grid(extent, cellsize, what = "centers")
my_formula <- formula(paste(column,"~1"))
idw_sf <- gstat::idw(formula = my_formula, groundtruth, newdata = samples, nmin = 1, nmax = nmax, maxdist = maxdist, idp = idp)
idw_matrix <- cbind(as.data.frame(st_coordinates(idw_sf)), pred = st_drop_geometry(idw_sf)[,1])
idw_matrix
}Nun könnt Ihr mit my_idw() den Datensatz luftqualitaet folgendermassen interpolieren.
my_idw(groundtruth = luftqualitaet, column = "value", cellsize = 10000, extent = schweiz)Folgende Parameter stehen Euch zur Verfügung:
- Notwendige Parameter:
groundtruth: Punktdatensatz mit den Messwerten (sf-Objekt)column: Name der Spalte mit den Messwerten (in Anführungs- und Schlusszeichen)cellsize: Zellgrösse des Output-Rasters
- Optionale Parameter
nmax: Maximale Anzahl Punkte, die für die Interpolation berücksichtigt werden sollen. Default:Inf(alle Werte im gegebenen Suchradius)maxdist: Suchradius, welcher für die Interpolation verwendet werden soll. DefaultInf(alle Werte bisnmax)idp: Inverse Distance Power: die Potenz, mit der der Nenner gesteigert werden soll. Default:2. Werte werden im Kehrwert des Quadrates gewichtet: \(\frac{1}{dist^{idp}}\).extent: Gebiet, für welches die Interpolation durchgeführt werden soll. Wenn nichts angegeben wird (DefaultNULL), wird die Ausdehnung vongroundtruthverwendet.
- Ouput
- der Output der Funktion ist eine
data.framemit 3 Spalten:X,YKoordinaten der interpolierten Wertepred: der interpolierte Wert
- der Output der Funktion ist eine
Beim Output handelt sich hier um einen Raster-ähnlichen Datentyp (siehe Vorlesung Spatial DataScience 1). Diesen können wir mit geom_raster mit ggplot visualisieren. Dafür müsst ihr in aes die X und Y Koordinaten angeben und der interpolierte Wert mit fill einfärben.
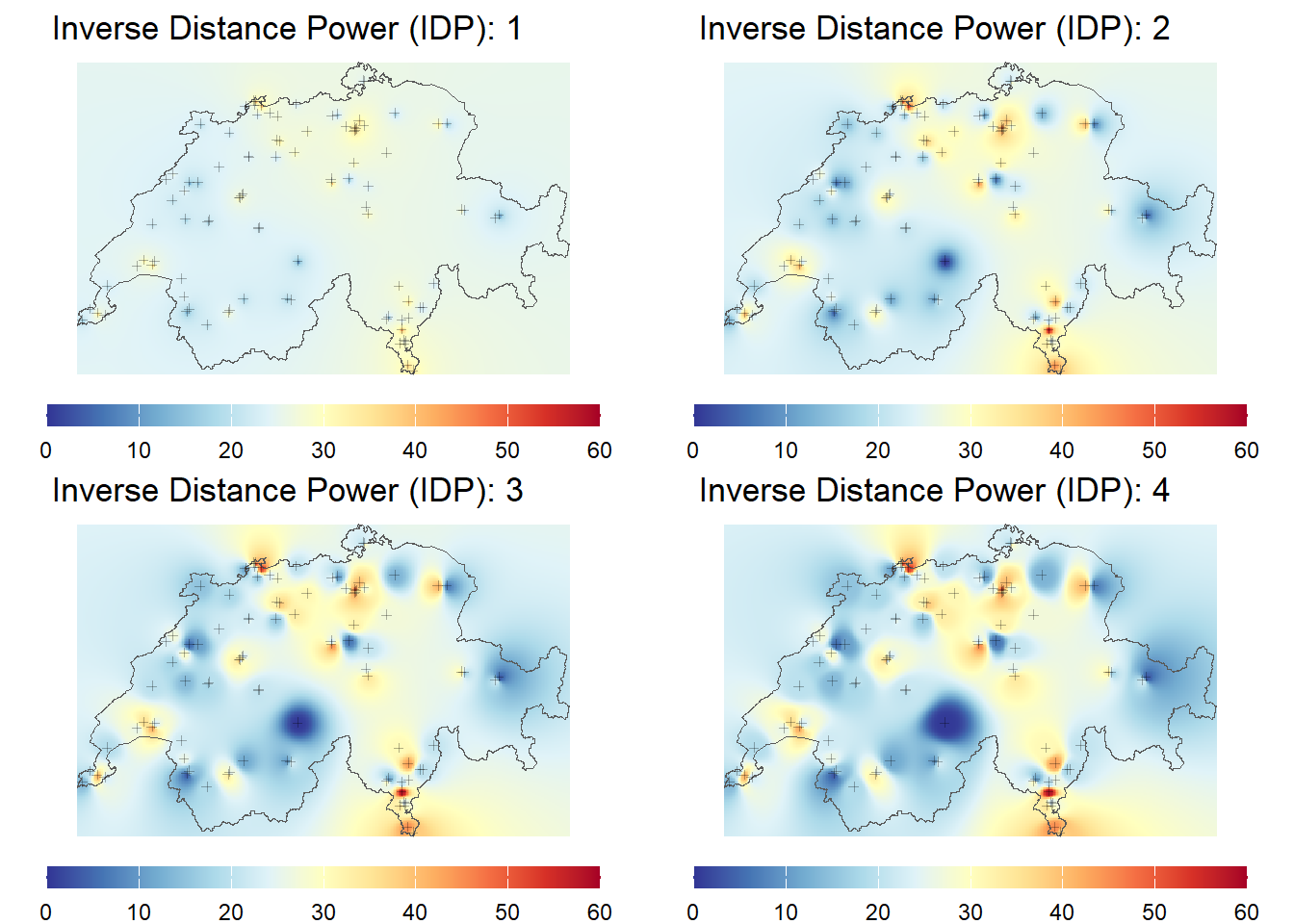
Aufgabe 1: Räumliche Interpolation mit IDW
Berechnet IDW-Interpolationen für die Luftqualitätsmessungen mit verschiedenen Parametern und visualisiert jeweils die Resultate. Experimentiert mit nmax sowie maxdist. Was stellt ihr fest?
Tips:
- Wählt am Anfang eine etwas konservative (grosse)
cellsizeund verringert diesen nur, wenn euer Rechner damit gut klar kommt. - Da der Output aus der Interpolation im gleichen Koordinatenbezugssystem ist wie
schweiz.gpkg, kann man diese beiden Datensätze im gleichenggplotdarstellen. Dafür müsst ihr die aesthetics (aes()) für jeden Layer einzeln setzen und nicht auf der Ebene vonggplot().
Aufgabe 2: Interpolation mit Nearest Neighbour
Eine weitere einfache Möglichkeit zur Interpolation bietet die Erstellung eines Voronoi-Diagrammes, auch als Thiessen Polygone oder Dirichlet-Zerlegung bekannt. sf liefert dazu die Funktion st_voronoi(), die einen Punktdatensatz annimmt und eben um die Punkte die Thiessen Polygone konstruiert. Dazu braucht es lediglich einen kleinen Vorverarbeitungsschritt: sf möchte für jedes Feature, also für jede Zeile in unserem Datensatz, ein Voronoidiagramm. Das macht bei uns wenig Sinn, weil jede Zeile nur aus einem Punkt besteht. Deshalb müssen wir vorher luftqualitaet mit st_union() von einem POINT- in ein MULTIPOINT-Objekt konvertieren, in welchem alle Punkte in einer Zeile zusammengefasst sind.
Musterlösung
luftqualitaet_union <- st_union(luftqualitaet)
thiessenpolygone <- st_voronoi(luftqualitaet_union)Musterlösung
ggplot() +
geom_sf(data = schweiz) +
geom_sf(data = thiessenpolygone, fill = NA)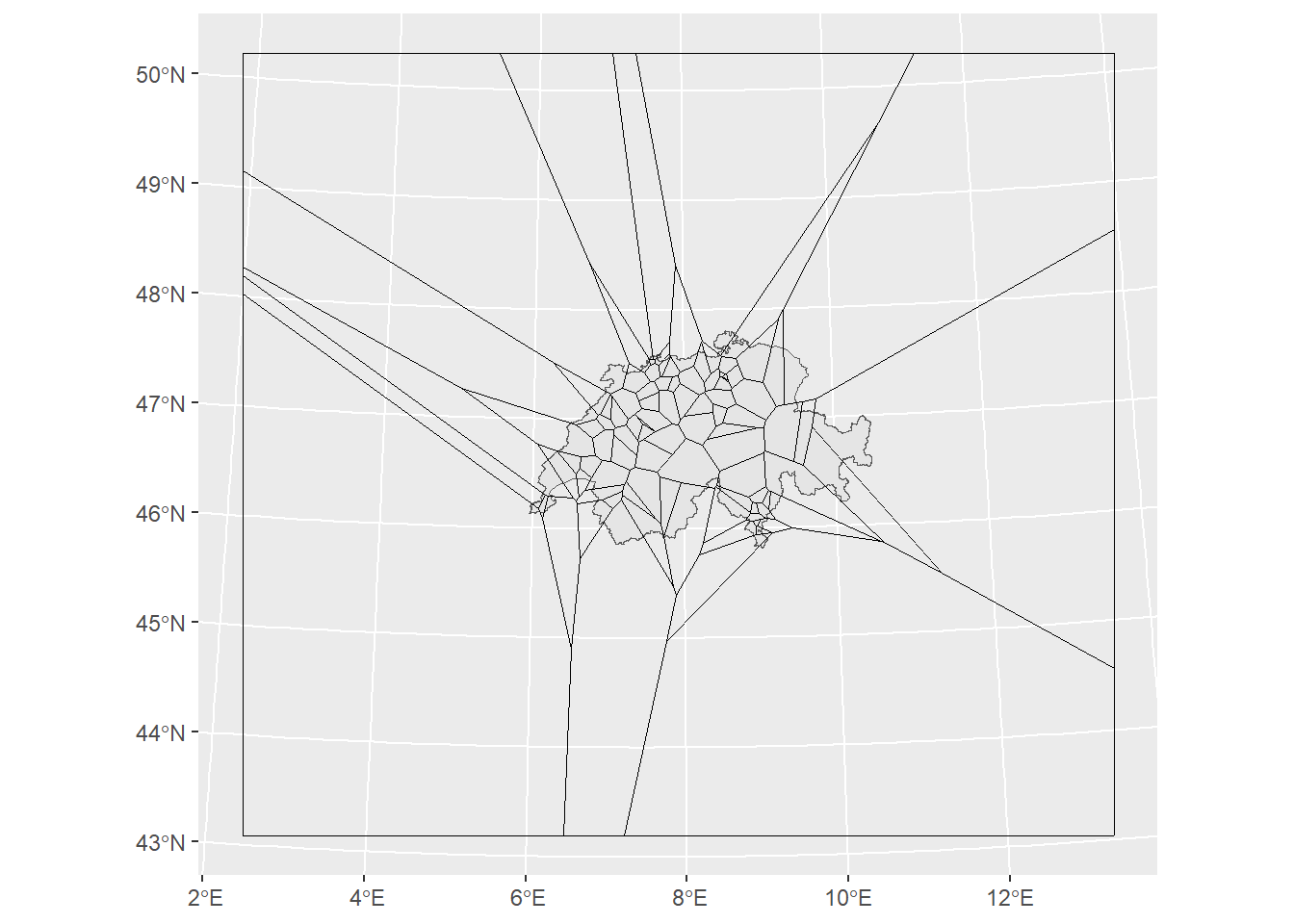
st_voronoi hat die Thiessen Polygone etwas weiter gezogen als wir sie wollen. Dies ist allerdings eine schöne Illustration der Randeffekte von Thiessen Polygonen, die zum Rand hin (wo es immer weniger Punkte hat) sehr gross werden können. Wir können die Polygone auf die Ausdehnung der Schweiz mit st_intersection() clippen. Vorher konvertieren wir mit st_collection_extract() die GEOMETRYCOLLECTION in POLYGON.
Musterlösung
thiessenpolygone <- st_collection_extract(thiessenpolygone)
thiessenpolygone_clip <- st_intersection(thiessenpolygone, schweiz)Musterlösung
ggplot() +
geom_sf(data = schweiz) +
geom_sf(data = thiessenpolygone_clip, fill = NA)
Jetzt müssen wir nur noch den jeweiligen Wert für jedes Polygon ermitteln. Dies erreichen wir wieder durch st_join. Auch hier ist noch ein kleiner Vorverarbeitungsschritt nötig: Wir konvertieren das sfc-Objekt (nur Geometrien) in ein sf-Objekt (Geometrien mit Attributtabelle).
Musterlösung
thiessenpolygone_clip <- st_as_sf(thiessenpolygone_clip)
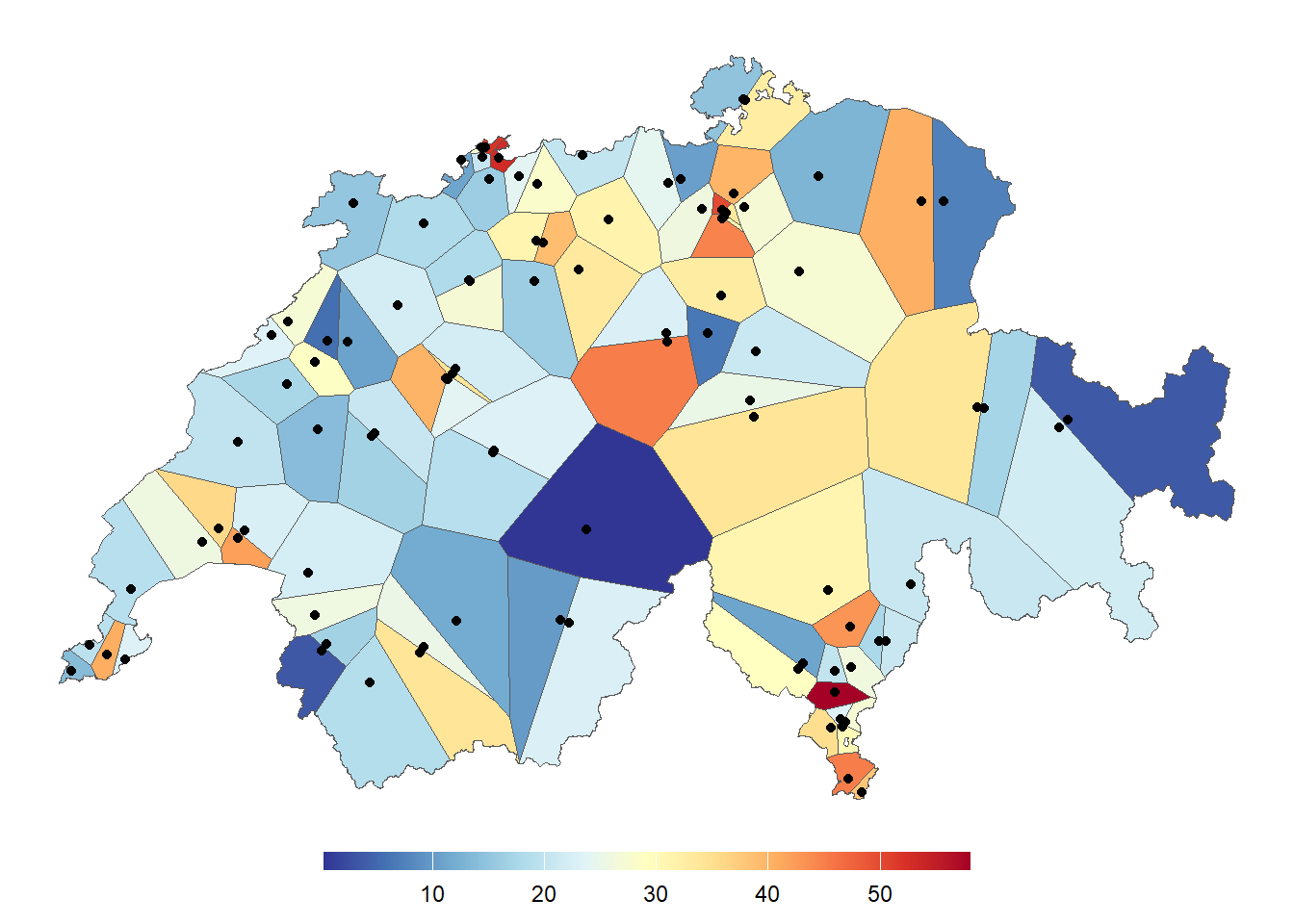
thiessenpolygone_clip <- st_join(thiessenpolygone_clip, luftqualitaet)Musterlösung
ggplot() +
geom_sf(data = schweiz) +
geom_sf(data = thiessenpolygone_clip, aes(fill = value)) +
geom_sf(data = luftqualitaet) +
scale_fill_gradientn(colours = rev(RColorBrewer::brewer.pal(11, "RdYlBu"))) +
theme_void() +
theme(
legend.position = "bottom", legend.title = element_blank(),
legend.key.width = unit(0.10, "npc"),
legend.key.height = unit(0.02, "npc")
)