DataUebung3 <- LifeCycleSavingsStatistik 3: Übung
Lineare und polynomische Regression
Aufgabenbeschreibung
In R gibt es zahlreiche eingebaute Datensätze. Diese sind direkt in R verfügbar und können ohne zusätzliche Downloads oder Installationen genutzt werden. In dieser Übung verwenden wir den Datensatz LifeCycleSavings. Du kannst den Datensatz z.B. mit folgendem Befehl als Objekt laden:
Der Datensatz enthält Informationen über die Sparquoten in 50 Ländern:
srSparquote (Savings Ratio; Anteil des Einkommens der gespart wird in Prozent)pop15Prozentsatz der Bevölkerung unter 15 Jahrenpop75Prozentsatz der Bevölkerung über 75 JahrendpiPro-Kopf-Einkommen
Du sollst nun untersuchen, ob und wie Sparquote von den anderen drei Variablen abhängt. Teste für jede erklärende Variable einzeln auf lineare und quadratische Zusammenhänge. Stelle die Ergebnisse grafisch dar und verfasse einen ausformulierten Methoden- und Ergebnisteil.
Demoscript herunterladen (.qmd)
R-Session vorbereiten
library(ggplot2)
library(patchwork)Daten anschauen
p1 <- ggplot(LifeCycleSavings, aes(x = pop15, y = sr)) +
geom_point()
p2 <- ggplot(LifeCycleSavings, aes(x = pop75, y = sr)) +
geom_point()
p3 <- ggplot(LifeCycleSavings, aes(x = dpi, y = sr)) +
geom_point()
p1+p2+p3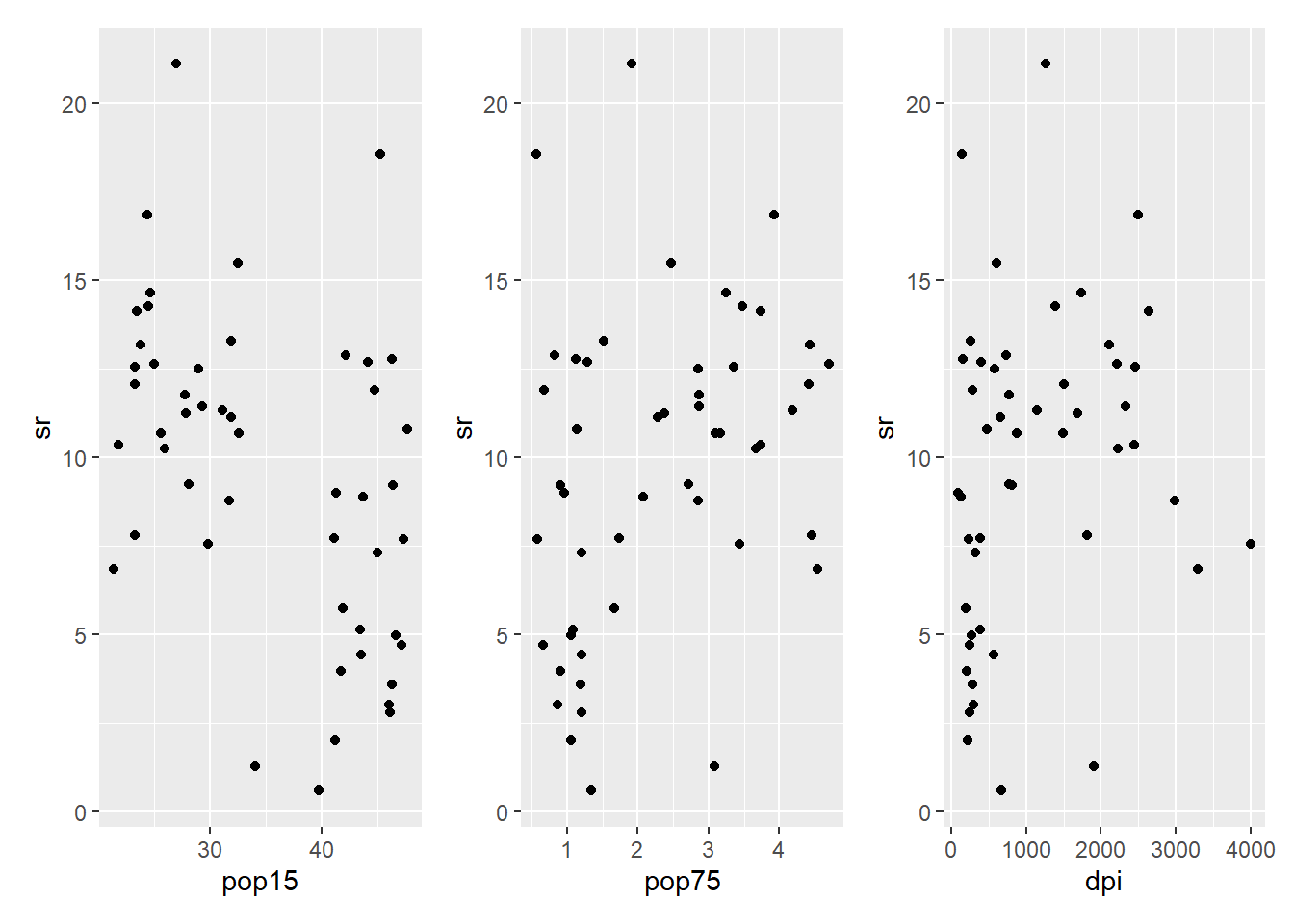
-> Zusammenhänge sind zu erahnen, aber die Streuung ist gross.
Modelle erstellen
lm_pop15 <- lm(sr ~ pop15 , data = LifeCycleSavings ) # Einfaches lineares Modell
lm_q_pop15 <- lm(sr ~ pop15 + I(pop15^2), data = LifeCycleSavings) # Modell mit quadratischem Term
lm_pop75 <- lm(sr ~ pop75, data = LifeCycleSavings ) # Einfaches lineares Modell
lm_q_pop75 <- lm(sr ~ pop75 + I(pop75^2), data = LifeCycleSavings) # Modell mit quadratischem Term
lm_dpi <- lm(sr ~ dpi , data = LifeCycleSavings ) # Einfaches lineares Modell
lm_q_dpi <- lm(sr ~ dpi + I(dpi^2), data = LifeCycleSavings) # Modell mit quadratischem TermModell-Outputs anschauen
lm_pop15 |> summary()
Call:
lm(formula = sr ~ pop15, data = LifeCycleSavings)
Residuals:
Min 1Q Median 3Q Max
-8.637 -2.374 0.349 2.022 11.155
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 17.49660 2.27972 7.675 6.85e-10 ***
pop15 -0.22302 0.06291 -3.545 0.000887 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 4.03 on 48 degrees of freedom
Multiple R-squared: 0.2075, Adjusted R-squared: 0.191
F-statistic: 12.57 on 1 and 48 DF, p-value: 0.0008866lm_q_pop15 |> summary()
Call:
lm(formula = sr ~ pop15 + I(pop15^2), data = LifeCycleSavings)
Residuals:
Min 1Q Median 3Q Max
-8.2918 -2.6062 0.2732 1.8186 11.0642
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 22.399363 13.358692 1.677 0.100
pop15 -0.522473 0.806247 -0.648 0.520
I(pop15^2) 0.004268 0.011455 0.373 0.711
Residual standard error: 4.067 on 47 degrees of freedom
Multiple R-squared: 0.2098, Adjusted R-squared: 0.1762
F-statistic: 6.241 on 2 and 47 DF, p-value: 0.003946-> Ein linearer negativer Zusammenhang ist vorhanden.
-> Kein quadratischer Zusammenhang.
lm_pop75 |> summary()
Call:
lm(formula = sr ~ pop75, data = LifeCycleSavings)
Residuals:
Min 1Q Median 3Q Max
-9.2657 -3.2295 0.0543 2.3336 11.8498
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 7.1517 1.2475 5.733 6.4e-07 ***
pop75 1.0987 0.4753 2.312 0.0251 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 4.294 on 48 degrees of freedom
Multiple R-squared: 0.1002, Adjusted R-squared: 0.08144
F-statistic: 5.344 on 1 and 48 DF, p-value: 0.02513lm_q_pop75 |> summary()
Call:
lm(formula = sr ~ pop75 + I(pop75^2), data = LifeCycleSavings)
Residuals:
Min 1Q Median 3Q Max
-9.6125 -3.2081 0.1644 2.2641 11.5023
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 5.9658 2.4752 2.410 0.0199 *
pop75 2.3997 2.3879 1.005 0.3201
I(pop75^2) -0.2608 0.4690 -0.556 0.5808
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 4.325 on 47 degrees of freedom
Multiple R-squared: 0.1061, Adjusted R-squared: 0.06803
F-statistic: 2.788 on 2 and 47 DF, p-value: 0.07172-> Ein linearer postiviver Zusammenhang ist vorhanden.
-> Kein quadratischer Zusammenhang.
lm_dpi |> summary()
Call:
lm(formula = sr ~ dpi, data = LifeCycleSavings)
Residuals:
Min 1Q Median 3Q Max
-9.1915 -3.6215 0.4418 2.8304 11.2790
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 8.5682306 0.9414690 9.101 5.04e-12 ***
dpi 0.0009964 0.0006366 1.565 0.124
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 4.416 on 48 degrees of freedom
Multiple R-squared: 0.04856, Adjusted R-squared: 0.02874
F-statistic: 2.45 on 1 and 48 DF, p-value: 0.1241lm_q_dpi |> summary()
Call:
lm(formula = sr ~ dpi + I(dpi^2), data = LifeCycleSavings)
Residuals:
Min 1Q Median 3Q Max
-10.663 -2.488 0.032 2.535 11.071
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 6.786e+00 1.207e+00 5.623 9.98e-07 ***
dpi 5.263e-03 2.008e-03 2.620 0.0118 *
I(dpi^2) -1.344e-06 6.028e-07 -2.230 0.0305 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 4.243 on 47 degrees of freedom
Multiple R-squared: 0.1396, Adjusted R-squared: 0.103
F-statistic: 3.813 on 2 and 47 DF, p-value: 0.02919-> Kein einfacher linearer Zusammenhang.
-> Ein quadratischer Zusammenhang ist vorhanden.
Modeldiagnostik
# Residualplots
par(mfrow = c(2, 2))
plot(lm_pop15)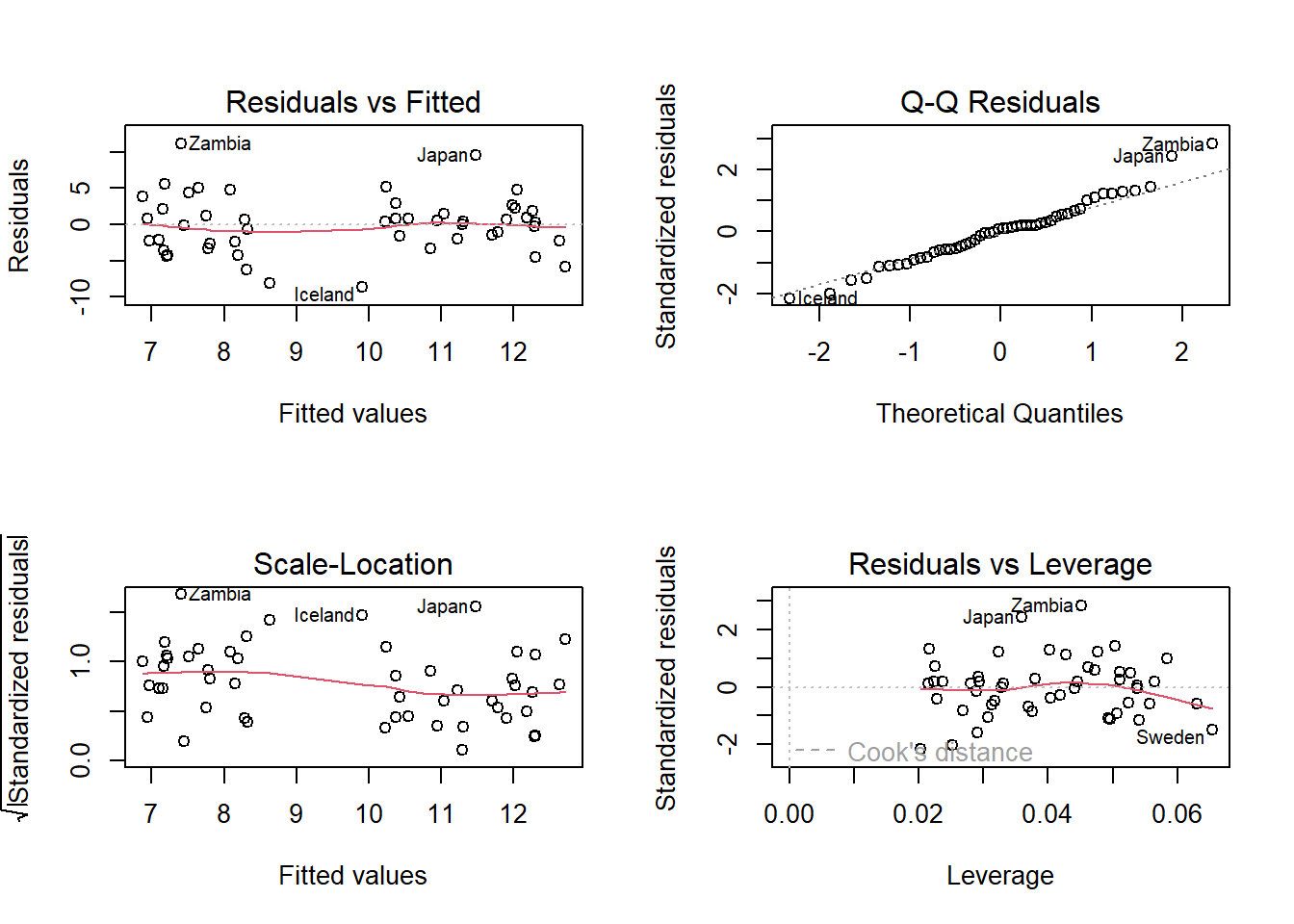
plot(lm_q_pop15)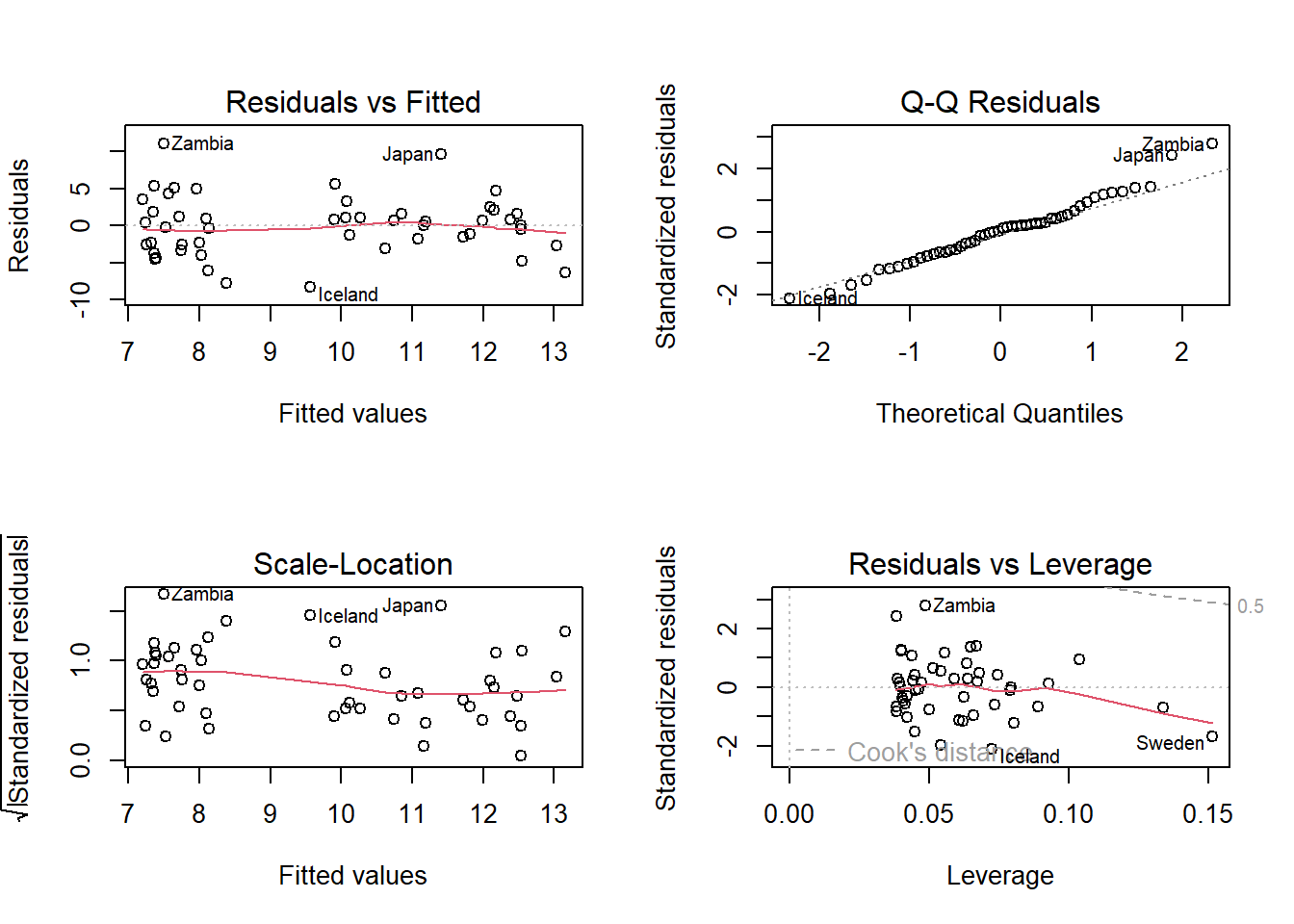
plot(lm_q_dpi)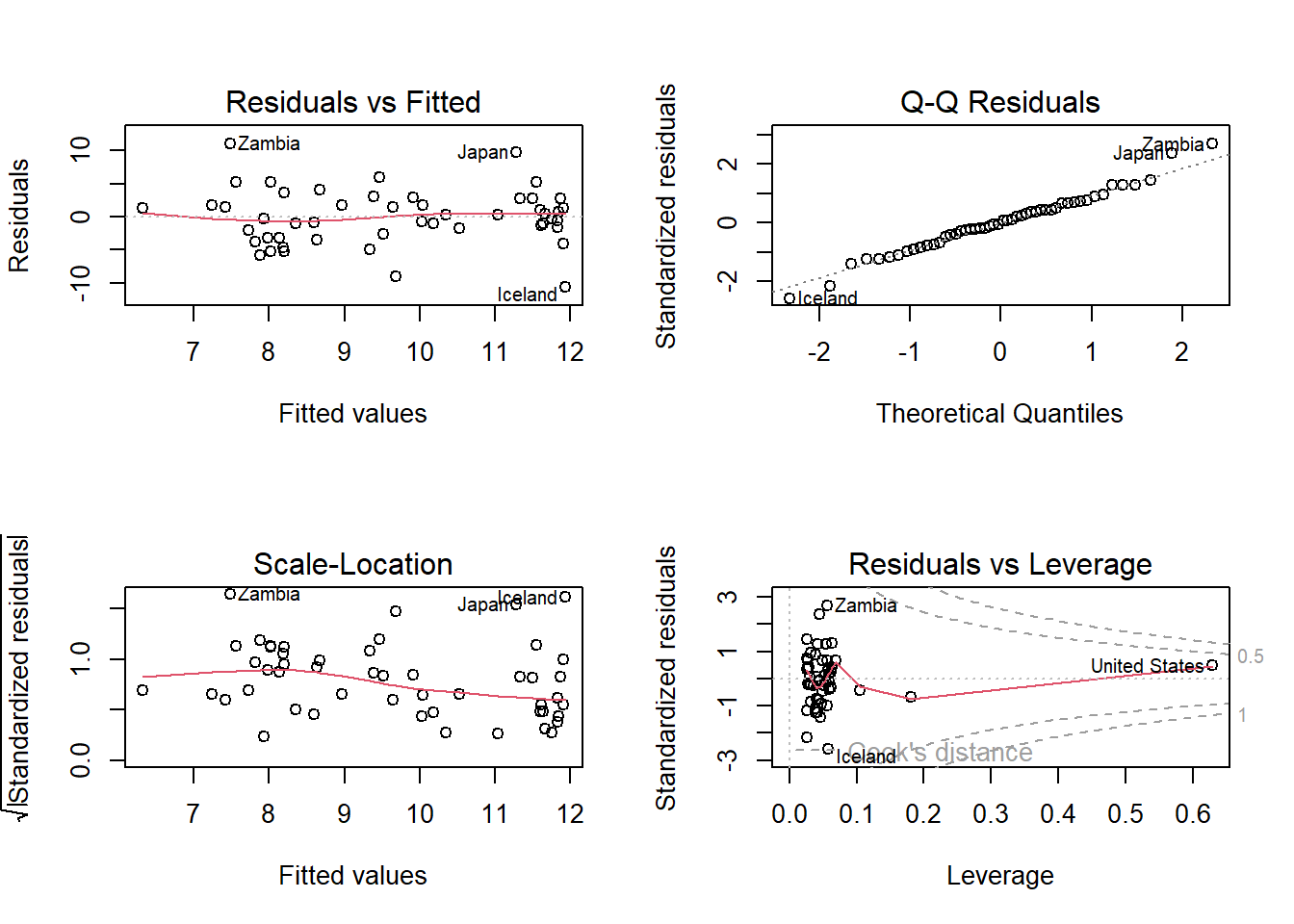
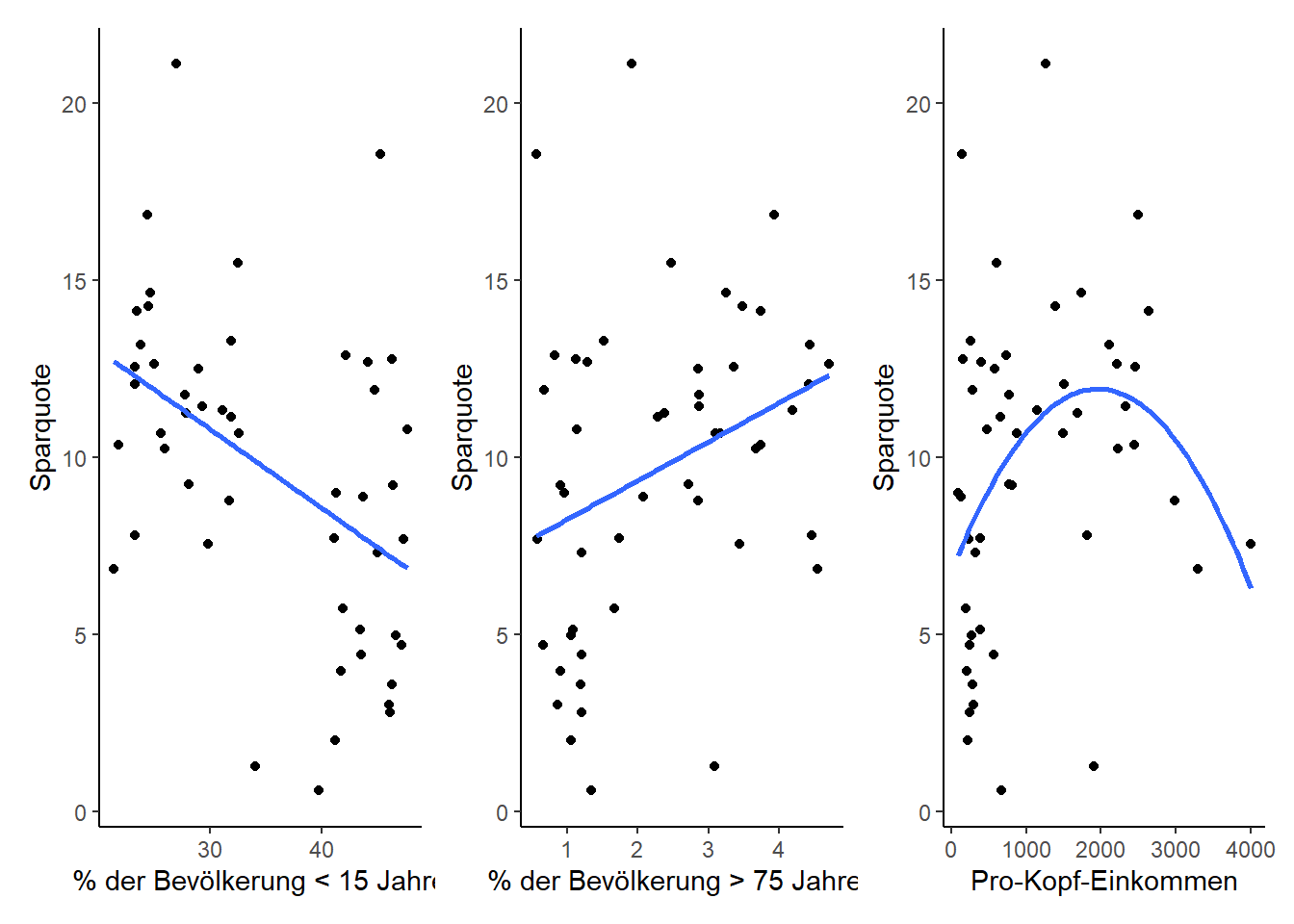
Darstellung der Ergebnisse
# Erstellen der Plots
p1 <- ggplot(LifeCycleSavings, aes(x = pop15, y = sr)) +
geom_point() +
geom_smooth(method = "lm", formula = y ~ x, se = FALSE) +
labs(x = "% der Bevölkerung < 15 Jahre",
y = "Sparquote") +
theme_classic()
p2 <- ggplot(LifeCycleSavings, aes(x = pop75, y = sr)) +
geom_point() +
geom_smooth(method = "lm", formula = y ~ x, se = FALSE) +
labs(x = "% der Bevölkerung > 75 Jahren",
y = "Sparquote") +
theme_classic()
p3 <- ggplot(LifeCycleSavings, aes(x = dpi, y = sr)) +
geom_point() +
geom_smooth(method = "lm", formula = y ~ x + I(x^2), se = FALSE) +
labs(x = "Pro-Kopf-Einkommen",
y = "Sparquote") +
theme_classic()
p1 + p2 + p3