Statistik 1: Demo

t-Test

Daten generieren und anschauen

# Je 10 Messwerte für Sorte a und b zu einem Data Frame im long-Format verbinden 
Messwerte_a <- c(20, 19, 25, 10, 8, 15, 13, 18, 11, 14) # Messwerte von Cultivar a
Messwerte_b <- c(12, 15, 16, 7, 8, 10, 12, 11, 13, 10) # Messwerte von Cultivar b
cultivar <- as.factor( c(rep("a", 10), rep("b", 10))) # Bezeichnug der Cultivare in der Tabelle
blume <- data.frame("cultivar" = cultivar, "size" = c(Messwerte_a, Messwerte_b)) # Data frame erstellen

# Boxplots

library(ggplot2)

ggplot(blume, aes(x = cultivar, y = size, fill = cultivar)) +
  geom_boxplot() + # Boxplots
  geom_dotplot(binaxis = "y", stackdir = "center", alpha = 0.5) # Datenpunkte darstellen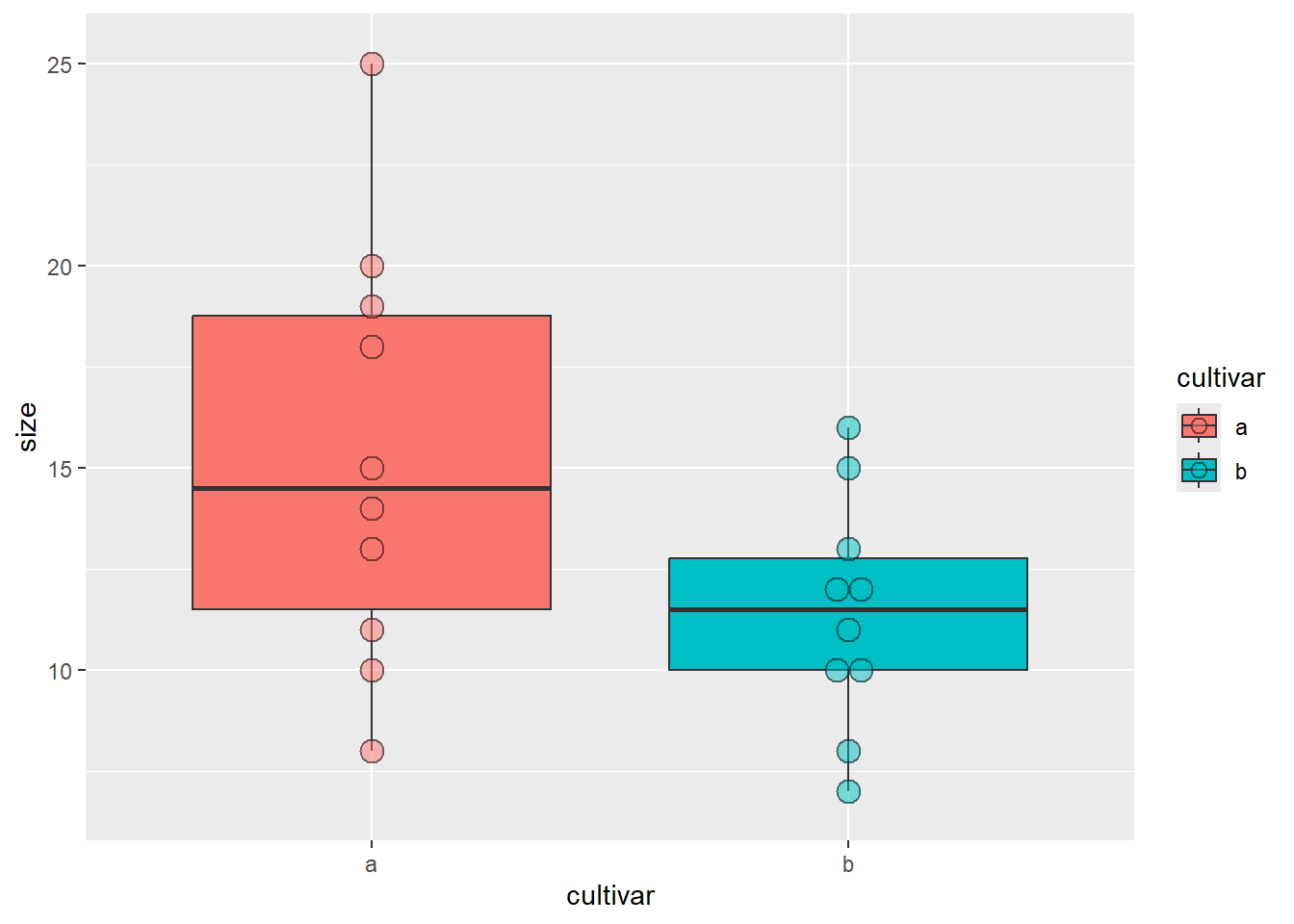

# Histogramme

ggplot(blume, aes(x = size, fill = cultivar)) +
  geom_histogram(binwidth = 2) +
  facet_wrap(~ cultivar)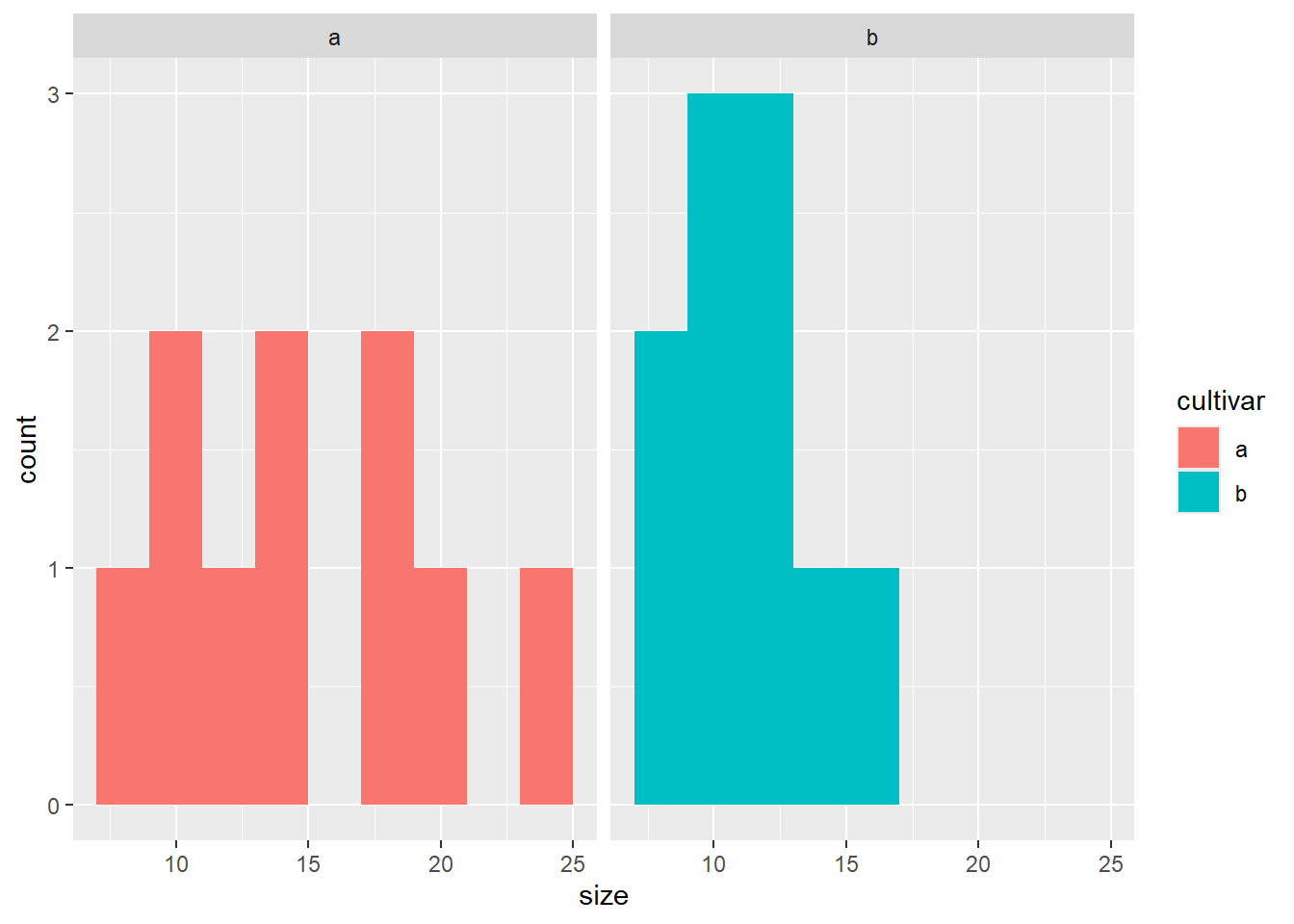

Zweiseitiger t-Test

# Links der Tilde ("~") steht immer die abhängige Variable, rechsts die erklärende(n) Variable(n)
# Alternativ kann man die Werte auch direkt in die t.test()-Funktion eigeben:
# t.test(Messwerte_a, Messwerte_b)

t.test(size ~ cultivar, data = blume) # Zweiseitig "Test auf a ≠ b" (default)


    Welch Two Sample t-test

data:  size by cultivar
t = 2.0797, df = 13.907, p-value = 0.05654
alternative hypothesis: true difference in means between group a and group b is not equal to 0
95 percent confidence interval:
 -0.1245926  7.9245926
sample estimates:
mean in group a mean in group b 
           15.3            11.4

Einseitiger t-Test

t.test(size ~ cultivar, alternative = "greater",  data = blume) # Einseitig "Test auf a > b"


    Welch Two Sample t-test

data:  size by cultivar
t = 2.0797, df = 13.907, p-value = 0.02827
alternative hypothesis: true difference in means between group a and group b is greater than 0
95 percent confidence interval:
 0.5954947       Inf
sample estimates:
mean in group a mean in group b 
           15.3            11.4

t.test(size ~ cultivar, alternative = "less",  data = blume) # Einseitig "Test auf a < b"


    Welch Two Sample t-test

data:  size by cultivar
t = 2.0797, df = 13.907, p-value = 0.9717
alternative hypothesis: true difference in means between group a and group b is less than 0
95 percent confidence interval:
     -Inf 7.204505
sample estimates:
mean in group a mean in group b 
           15.3            11.4

Klassischer t-Test vs. Welch Test

# Varianzen gleich: klassischer t-Test
t.test(size ~ cultivar, var.equal = TRUE, data = blume)


    Two Sample t-test

data:  size by cultivar
t = 2.0797, df = 18, p-value = 0.05212
alternative hypothesis: true difference in means between group a and group b is not equal to 0
95 percent confidence interval:
 -0.03981237  7.83981237
sample estimates:
mean in group a mean in group b 
           15.3            11.4

# Varianzen ungleich: Welch's t-Test (siehe Titelzeile des R-Outputs!)
t.test(size ~ cultivar, data = blume) # dasselbe wie var.equal = FALSE


    Welch Two Sample t-test

data:  size by cultivar
t = 2.0797, df = 13.907, p-value = 0.05654
alternative hypothesis: true difference in means between group a and group b is not equal to 0
95 percent confidence interval:
 -0.1245926  7.9245926
sample estimates:
mean in group a mean in group b 
           15.3            11.4

Gepaarter t-Test

# Gepaarter t-Test: erster Wert von a wird mit erstem Wert von
# b gepaart, zweiter Wert von a mit zweitem von b ect.

t.test(Messwerte_a, Messwerte_b, paired = TRUE) # für gepaarten t-Test funktioniert Notation "size ~ cultivar" nicht


    Paired t-test

data:  Messwerte_a and Messwerte_b
t = 3.4821, df = 9, p-value = 0.006916
alternative hypothesis: true mean difference is not equal to 0
95 percent confidence interval:
 1.366339 6.433661
sample estimates:
mean difference 
            3.9

Binomialtest

In Klammern übergibt man die Anzahl der Erfolge und die Stichprobengrösse

binom.test(84, 200) # Anzahl Frauen im Nationalrat (≙ 42.0 %; Stand 2019)


    Exact binomial test

data:  84 and 200
number of successes = 84, number of trials = 200, p-value = 0.02813
alternative hypothesis: true probability of success is not equal to 0.5
95 percent confidence interval:
 0.3507439 0.4916638
sample estimates:
probability of success 
                  0.42

binom.test(116, 200) # Anzahl Männer im Nationalrat (≙ 58.0 %; Stand 2019)


    Exact binomial test

data:  116 and 200
number of successes = 116, number of trials = 200, p-value = 0.02813
alternative hypothesis: true probability of success is not equal to 0.5
95 percent confidence interval:
 0.5083362 0.6492561
sample estimates:
probability of success 
                  0.58

binom.test(3, 7) # Anzahl Frauen im Bundesrat (≙ 42.9 %; Stand 2019)


    Exact binomial test

data:  3 and 7
number of successes = 3, number of trials = 7, p-value = 1
alternative hypothesis: true probability of success is not equal to 0.5
95 percent confidence interval:
 0.09898828 0.81594843
sample estimates:
probability of success 
             0.4285714

Chi-Quadrat-Test & Fishers Test

Ermitteln des kritischen Wertes

Direkter Test in R (dazu Werte als Matrix nötig)

# Matrix mit Haarfarbe&Augenfarbe-Kombinationen erstellen
# 38 blond&blau, 14 dunkel&blau, 11 blond&braun, 51 dunkel&braun
count <- matrix(c(38, 14, 11, 51), nrow = 2)
count # Check

     [,1] [,2]
[1,]   38   11
[2,]   14   51

rownames(count) <- c("blond", "dunkel") # Benennen für Übersicht
colnames(count) <- c("blau", "braun") #  Benennen für Übersicht
count # Check

       blau braun
blond    38    11
dunkel   14    51

# Tests durchführen
chisq.test(count)


    Pearson's Chi-squared test with Yates' continuity correction

data:  count
X-squared = 33.112, df = 1, p-value = 8.7e-09

fisher.test(count)


    Fisher's Exact Test for Count Data

data:  count
p-value = 2.099e-09
alternative hypothesis: true odds ratio is not equal to 1
95 percent confidence interval:
  4.746351 34.118920
sample estimates:
odds ratio 
  12.22697