library("dplyr")
library("ggplot2")
library("sf")
zweitwohnung_kanton <- read_sf("datasets/rauman/zweitwohnungsinitiative.gpkg", layer = "kanton")Rauman 4: Übung
Heute berechnen wir Morans \(I\), also ein globales Mass für Autokorrelation, für die Abstimmungsresultate der Zweitwohnungsinitiative. Dieser Wert beschreibt, ob Kantone, die nahe beieinanderliegen, ähnliche Abstimmungswerte haben. Hierfür verwenden wir den Datensatz zweitwohnungsinitiative.gpkg.
Das Geopackage beinhaltet 3 Layers (siehe st_layers(zweitwohnung_kanton)). In jedem Layer sind die Abstimmungsresultate auf eine andere politische Ebene aggregiert. Wir starten mit der Aggregationsstufe “kanton”.
p <- ggplot(zweitwohnung_kanton) +
geom_sf(aes(fill = ja_in_percent), colour = "white", lwd = 0.2) +
scale_fill_gradientn("Ja-Anteil",
colours = RColorBrewer::brewer.pal(11, "RdYlGn"),
limits = c(0, 100),
) +
labs(title = "Zweitwohnungsinititiative (2012)", subtitle = "Anteil Ja-Stimmen") +
theme(legend.position = "bottom")
p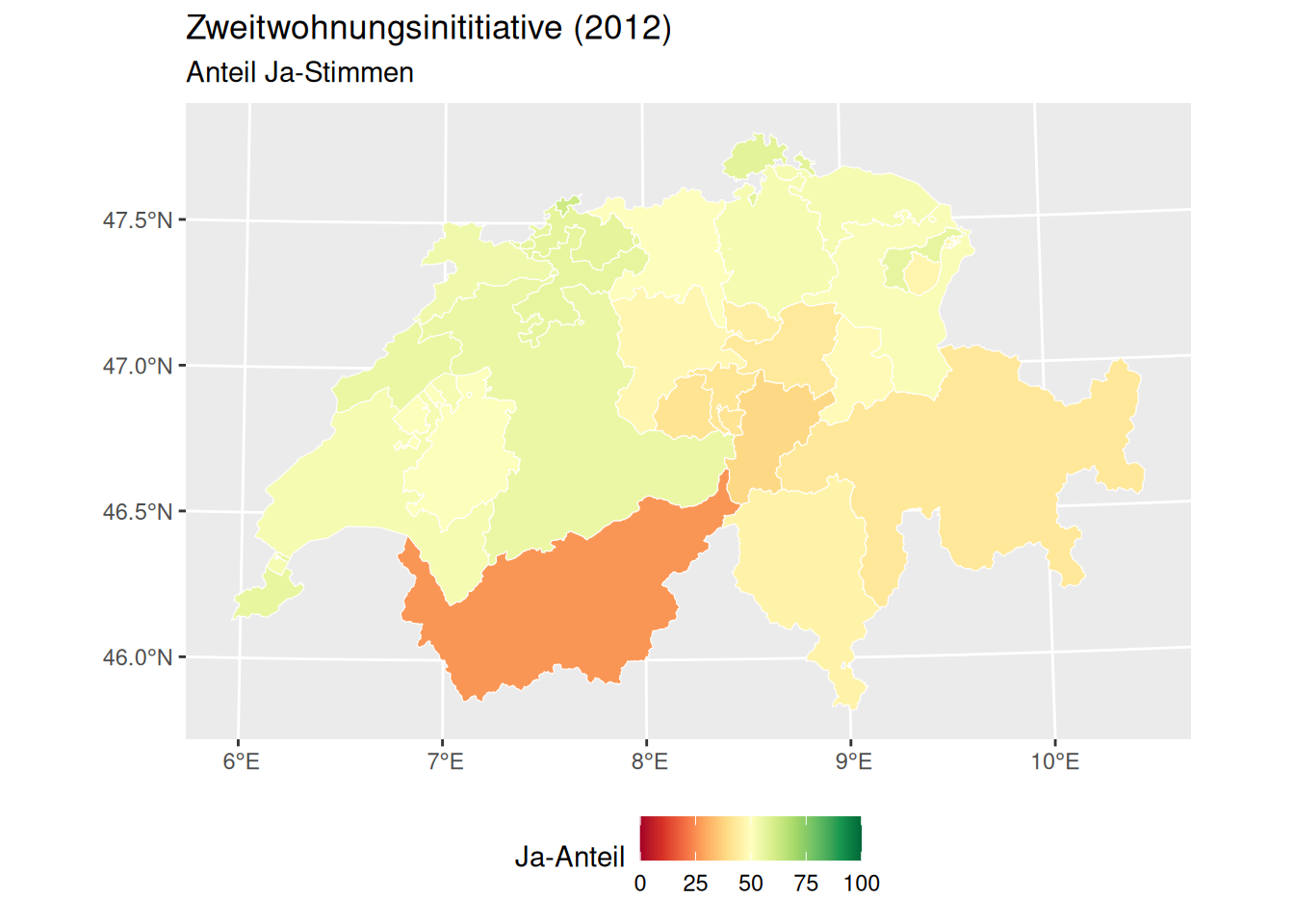
Für die Berechnung von Morans \(I\) benutzen wir kein externes Package, sondern erarbeiten uns alles selber, basierend auf der Formel von Moran’s \(I\):
\[ \begin{aligned} \text{Morans } I &= \frac{\color{cyan}n}{\color{cyan}\sum_{i=1}^n (y_i - \bar{y})^2} \times \frac{\color{red}\sum_{i=1}^n \sum_{j=1}^n w_{ij}(y_i - \bar{y})(y_j - \bar{y})}{\color{cyan}\sum_{i=1}^n \sum_{j=1}^n w_{ij}} \\ \\ &= \frac{\color{cyan}\text{zaehler1}}{\color{cyan}\text{nenner1}}\times\frac{\color{red}\text{zaehler2}}{\color{cyan}\text{nenner2}} \end{aligned} \tag{40.1}\]
Rot markiert entpricht der Summe der gewichteten Ähnlichkeitsmatrix aus der Vorlesung. Alles blaue ist relativ trivial und dient lediglich der Normalisierung auf die Werte -1 bis +1. Die Begriffe zaehler1, nenner1 usw. sind die Variablen, die wir in R für die jeweiligen Berechnungen nutzen werden und dienen lediglich der Orientierung. Zudem gilt:
- \(n\): Anzahl räumliche Objekte (hier: 26 Kantone)
- \(y\): die untersuchte Variabel (hier: Ja-Anteil in %)
- \(\bar{y}\): Mittelwert der untersuchten Variabel
- \(w_{ij}\): die Gewichtsmatrix
Aufgabe 1: Morans \(I\) für Kantone
Gewichtete Ähnlichkeitsmatrix
Widmen wir uns dem Kern von Morans \(I\), der Berechnung der gewichteten Ähnlichkeitsmatrix.
Nachbarschaftsmatrix \(w_{ij}\)
\[\text{Morans } I = \frac{n}{\sum_{i=1}^n (y_i - \bar{y})^2} \times \frac{\sum_{i=1}^n \sum_{j=1}^n {\color{red}w_{ij}}(y_i - \bar{y})(y_j - \bar{y})}{\sum_{i=1}^n \sum_{j=1}^n w_{ij}}\]
\(w\) beschreibt die räumlichen Gewichte der Kantone (den “Schalter” aus der Vorlesung). \(w_{ij}\) ist das Gewicht vom Kanton \(i\) im Vergleich zum Kanton \(j\). Sind Kantone \(i\) und \(j\) räumlich nah, gilt ein Gewicht von 1, sind sie weit entfernt, gilt ein Gewicht von 0. Dabei ist die Definition von “räumlich nah” nicht festgelegt. Denkbar wären verschiedene Optionen (siehe Vorlesung). Wir werden es mit die Bedigungen touches verwenden. Die Funktion st_touches prüft zwischen allen Kantonen, ob sie sich berühren. Mit der Option sparse = TRUE wird eine 26x26 Kreuzmatrix erstellt, wo jeder Kanton mit jedem anderen verglichen wird. Berühren sie sich, steht in der entsprechenden Stelle der Wert TRUE, was in R gleichbedeutend ist wie 1. Berühren sie sich nicht, steht der Wert FALSE, was gleichbedeutend ist wie 0.
# st_touches berechnet eine Kreuzmatrix aller Objekte
w_ij <- st_touches(zweitwohnung_kanton, sparse = FALSE)
# Schauen wir uns die Matrix mal an
# (aus Platzmangen beschränken wir uns auf die ersten 5 Zeilen und Spalten
# in RStudio könnt ihr mit View(w_ij) die gesamte Matrix anschauen)
w_ij[1:5, 1:5]
## [,1] [,2] [,3] [,4] [,5]
## [1,] FALSE FALSE FALSE FALSE TRUE
## [2,] FALSE FALSE TRUE TRUE FALSE
## [3,] FALSE TRUE FALSE FALSE TRUE
## [4,] FALSE TRUE FALSE FALSE TRUE
## [5,] TRUE FALSE TRUE TRUE FALSEDie erste Zeile entspricht dem ersten Kanton in zweitwohnung_kanton, die zweite Zeile dem zweiten Kanton usw. Das gleiche gilt für die Spalten. Um die Kreuzmatrix besser interpretieren zu können, können wir die Namen aus der Spalte KANTONSNAME verwenden, um die Zeilen und Spalten unserer Kreuzmatrix zu benennen.
rownames(w_ij) <- zweitwohnung_kanton$kuerzel
colnames(w_ij) <- zweitwohnung_kanton$kuerzel
w_ij[1:5, 1:5]
## ZH BE LU UR SZ
## ZH FALSE FALSE FALSE FALSE TRUE
## BE FALSE FALSE TRUE TRUE FALSE
## LU FALSE TRUE FALSE FALSE TRUE
## UR FALSE TRUE FALSE FALSE TRUE
## SZ TRUE FALSE TRUE TRUE FALSE
# Alterantiv: mit View(w_ij)Attributs-Ähnlichkeitsmatrix \(c_{ij}\)
\[\text{Morans } I = \frac{n}{\sum_{i=1}^n (y_i - \bar{y})^2} \times \frac{\sum_{i=1}^n \sum_{j=1}^n w_{ij}{\color{red}(y_i - \bar{y})(y_j - \bar{y})}}{\sum_{i=1}^n \sum_{j=1}^n w_{ij}}\]
Um die Attributs-Ähnlichkeit zwischen zwei Kantonen zu bestimmen, subtrahieren wir von jedem Kanton den Mittelwert aller Kantone und multiplizieren die beiden Differenzen. Die Funktion tcrossprod() erstellt diese Kreuzmatrix mit den multiplizierten Differenzen.
# speichere die Variable in einem neuen Vektor
y <- zweitwohnung_kanton$ja_in_percent
y_diff <- y - mean(y) # erstellt ein Vector mit 26 Werten
c_ij <- tcrossprod(y_diff) # erstellt eine Matrix 26x26
# Zeilen- und Spaltennamen hinzufügen
rownames(c_ij) <- zweitwohnung_kanton$kuerzel
colnames(c_ij) <- zweitwohnung_kanton$kuerzel
c_ij[1:5, 1:5]
## ZH BE LU UR SZ
## ZH 9.094864 16.48350 -6.677609 -32.70370 -20.09778
## BE 16.483499 29.87463 -12.102474 -59.27206 -36.42515
## LU -6.677609 -12.10247 4.902818 24.01163 14.75614
## UR -32.703697 -59.27206 24.011629 117.59734 72.26846
## SZ -20.097782 -36.42515 14.756145 72.26846 44.41197Berechnung von zaehler2
\[\text{Morans } I = \frac{n}{\sum_{i=1}^n (y_i - \bar{y})^2} \times \frac{\color{red}\sum_{i=1}^n \sum_{j=1}^n w_{ij}(y_i - \bar{y})(y_j - \bar{y})}{\sum_{i=1}^n \sum_{j=1}^n w_{ij}}\]
Der gesamte Term zaehler2 ist die Summe aus der Multiplikation von w_ij und c_ij.
# Matrix multiplikation
cw_ij <- w_ij * c_ij
# Summe bilden
zaehler2 <- sum(cw_ij)
zaehler2
## [1] 1980.689Normalisieren
Um das Resultat aus der bisherigen Berechung auf einen Wert von -1 bis +1 zu normalisieren, müssen wir noch folgende Terme berechnen:
\[\text{Morans } I = \frac{\color{cyan}n}{\color{cyan}\sum_{i=1}^n (y_i - \bar{y})^2} \times \frac{\sum_{i=1}^n \sum_{j=1}^n w_{ij}(y_i - \bar{y})(y_j - \bar{y})}{\color{cyan}\sum_{i=1}^n \sum_{j=1}^n w_{ij}} \]
Berechnung von \(n\) (zaehler1)
Der Term zaehler1 resp. n entspricht der Anzahl Objekte (hier: Kantone) in unserem Datensatz.
zaehler1 <- n <- nrow(zweitwohnung_kanton)
zaehler1
## [1] 26Abweichung vom Mittelwert (nenner1)
Wir haben bereits in der Berechnung der Attributs-Ähnlichkeit die Differenz zum Mittelwert berechnet. Für nenner1 müssen wir diesen lediglich quadrieren und die Resultate summieren.
\[\text{Morans } I = \frac{n}{\color{cyan}\sum_{i=1}^n (y_i - \bar{y})^2} \times \frac{\sum_{i=1}^n \sum_{j=1}^n w_{ij}(y_i - \bar{y})(y_j - \bar{y})}{\sum_{i=1}^n \sum_{j=1}^n w_{ij}}\]
# Di bereits berechneten Abweichungen müssen wir quadrieren:
y_diff2 <- y_diff^2
# Und danach die Summe bilden:
nenner1 <- sum(y_diff2)Summe der Gewichte (nenner2)
\[\text{Morans } I = \frac{n}{\sum_{i=1}^n (y_i - \bar{y})^2} \times \frac{\sum_{i=1}^n \sum_{j=1}^n w_{ij}(y_i - \bar{y})(y_j - \bar{y})}{\color{cyan}\sum_{i=1}^n \sum_{j=1}^n w_{ij}}\]
Im Term nenner2 müssen wir lediglich die Gewichte w_ij summieren.
nenner2 <- sum(w_ij)Auflösung der Formel
Nun haben wir alle Bestandteile von Morans \(I\) berechnet und müssen diese nur noch zusammenrechnen.
MI_kantone <- zaehler1 / nenner1 * zaehler2 / nenner2
MI_kantone
## [1] 0.3126993Der Global Morans \(I\) für die Abstimmungsdaten beträgt auf Kantonsebene also 0.31. Wie interpretiert ihr dieses Resultate? Was erwartet ihr für eine Resultat auf Bezirksebene?
Aufgabe 2: Morans I für Bezirke berechnen
Nun könnt ihr Morans \(I\) auf der Ebene der Bezirke und untersuchen, ob und wie sich Morans \(I\) verändert. Importiert dazu den Layer bezirk aus dem Datensatz zweitwohnungsinitiative.gpkg. Visualisiert in einem ersten Schritt die Abstimmungsresultate. Formuliert nun eine Erwartungshaltung: Ist Morans \(I\) auf der Ebene Bezirke tiefer oder Höher als auf der Ebene Kantone?
Erstellt aus dem erarbeiten Workflow eine function um Morans I auf der Basis von einem sf Objekt sowie einer Spalte dessen zu berechnen.
Musterlösung
morans_i <- function(sf_object, col) {
library("sf")
w_ij <- st_touches(sf_object, sparse = FALSE)
y <- sf_object[, col, drop = TRUE]
y_diff <- y - mean(y)
c_ij <- tcrossprod(y_diff)
cw_ij <- w_ij * c_ij
zaehler2 <- sum(cw_ij)
zaehler1 <- n <- nrow(sf_object)
y_diff2 <- y_diff^2
nenner1 <- sum(y_diff2)
nenner2 <- sum(w_ij)
morans_i_result <- zaehler1 / nenner1 * zaehler2 / nenner2
return(morans_i_result)
}
# Kommentar
# Wir können hier nicht das $ Zeichen verwenden, weil "col" ein String ist.
# Mit der doppelten, eckigen klammer stellen wir sicher, dass y erstens ein
# Vektor ist (schau dir "y" an wenn du nur eine Klammer verwendest)Musterlösung
zweitwohnung_bezirke <- read_sf("datasets/rauman/zweitwohnungsinitiative.gpkg", "bezirk")
MI_bezirke <- morans_i(zweitwohnung_bezirke, "ja_in_percent")Musterlösung
p2 <- ggplot(zweitwohnung_bezirke) +
geom_sf(aes(fill = ja_in_percent), colour = "white", lwd = 0.2) +
scale_fill_gradientn("Ja Anteil", colours = RColorBrewer::brewer.pal(11, "RdYlGn"), limits = c(0, 100)) +
theme(legend.position = "none") +
labs(
title = paste("Zweitwohnungsinitiative (2012), Ja-Stimmen-Anteil auf Ebene Bezirk"),
subtitle = paste("Global Morans I: ", "??")
)
p1 <- p + labs(
title = paste("Zweitwohnungsinitiative (2012), Ja-Stimmen-Anteil auf Ebene Kanton"),
subtitle = paste("Global Morans I: ", round(MI_kantone, 2))
) +
theme(legend.position = "none")
p1
p2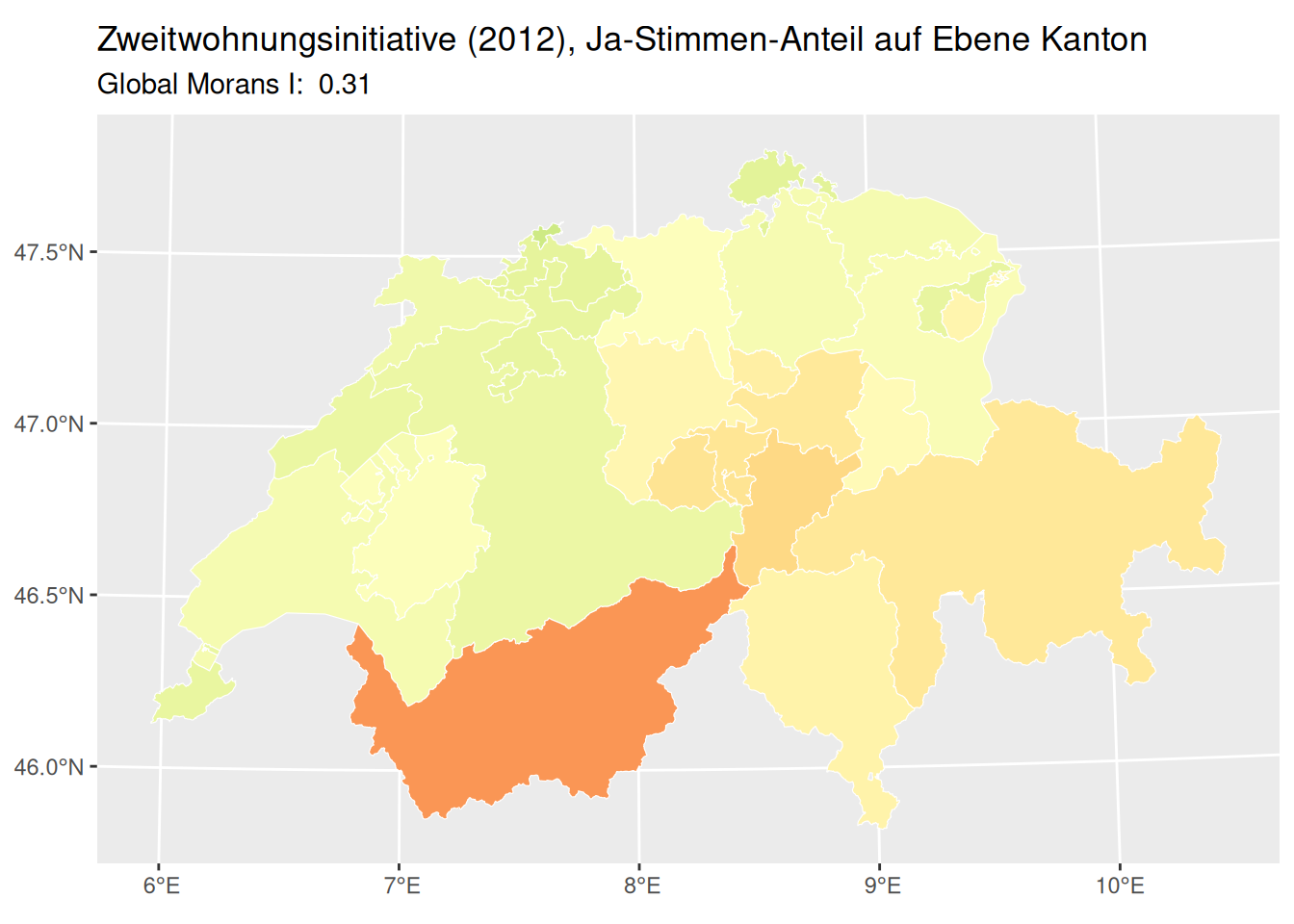

Musterlösung
library("cowplot")
(p +
theme(legend.key.width = unit(2, "cm"), legend.title = element_blank())
) |>
get_legend() |>
ggdraw()
