library("sf")
library("terra")
library("dplyr")
library("readr")
library("ggplot2")
library("PerformanceAnalytics")
library("pastecs")
library("lme4")
library("bbmle")
library("MuMIn")
library("MASS")Variablenselektion Multivariate Modelle
Libraries laden
Variablenselektion
→ Vorgehen analog Coppes u. a. (2017)
Aufgabe 1
Mit dem folgenden Code kann eine simple Korrelationsmatrix aufgebaut werden, vergl. Aufgabe 5 vorangehende Woche
DF_mod <- read_delim("datasets/fallstudie_n/Aufgabe4_Datensatz_Habitatnutzung_Modelle_241028.csv", delim = ";")
DF_mod_day <- DF_mod |>
filter(time_of_day == "day")
round(cor(DF_mod_day[, 5:12], method = "pearson"), 2)
## slope topo_pos dist_road_trails dist_road_only dist_sett
## slope 1.00 0.09 0.31 0.34 0.14
## topo_pos 0.09 1.00 0.06 0.09 0.08
## dist_road_trails 0.31 0.06 1.00 0.93 -0.05
## dist_road_only 0.34 0.09 0.93 1.00 -0.08
## dist_sett 0.14 0.08 -0.05 -0.08 1.00
## forest_prop 0.29 0.01 -0.03 -0.05 0.50
## us_2014 0.28 -0.04 0.03 0.04 0.06
## os_2014 0.45 0.06 -0.03 -0.01 0.34
## forest_prop us_2014 os_2014
## slope 0.29 0.28 0.45
## topo_pos 0.01 -0.04 0.06
## dist_road_trails -0.03 0.03 -0.03
## dist_road_only -0.05 0.04 -0.01
## dist_sett 0.50 0.06 0.34
## forest_prop 1.00 0.34 0.76
## us_2014 0.34 1.00 0.47
## os_2014 0.76 0.47 1.00
# hier kann die Schwelle für die Korrelation gesetzt werden, 0.7 ist eher liberal /
# 0.5 konservativ
cor <- round(cor(DF_mod_day[, 5:12], method = "pearson"), 2)
cor[abs(cor) < 0.7] <- 0
cor
## slope topo_pos dist_road_trails dist_road_only dist_sett
## slope 1 0 0.00 0.00 0
## topo_pos 0 1 0.00 0.00 0
## dist_road_trails 0 0 1.00 0.93 0
## dist_road_only 0 0 0.93 1.00 0
## dist_sett 0 0 0.00 0.00 1
## forest_prop 0 0 0.00 0.00 0
## us_2014 0 0 0.00 0.00 0
## os_2014 0 0 0.00 0.00 0
## forest_prop us_2014 os_2014
## slope 0.00 0 0.00
## topo_pos 0.00 0 0.00
## dist_road_trails 0.00 0 0.00
## dist_road_only 0.00 0 0.00
## dist_sett 0.00 0 0.00
## forest_prop 1.00 0 0.76
## us_2014 0.00 1 0.00
## os_2014 0.76 0 1.00Aufgabe 2
Skalieren der Variablen, damit ihr Einfluss vergleichbar wird (Befehl scale(); Problem verschiedene Skalen der Variablen (bspw. Neigung in Grad, Distanz in Metern)); Umwandeln der Reh-ID in einen Faktor, damit dieser als Random Factor ins Model eingespiesen werden kann.
DF_mod_day <- DF_mod_day |>
mutate(
slope_scaled = scale(slope),
topo_pos_scaled = scale(topo_pos),
us_scaled = scale(us_2014),
os_scaled = scale(os_2014),
forest_prop_scaled = scale(forest_prop),
dist_road_trails_scaled = scale(dist_road_trails),
dist_road_only_scaled = scale(dist_road_only),
dist_sett_scaled = scale(dist_sett),
id = as.factor(id)
)Aufgabe 3
Selektion der Variablen in einem univariaten Model
Ein erstes GLMM (Generalized Linear Mixed Effects Modell) aufbauen: Funktion und Modelformel
wichtige Seite auf der man viele Hilfestellungen zu GLMM’s finden kann.
# wir werden das package lme4 mit der Funktion glmer verwenden
# die Hilfe von glmer aufrufen: ?glmer
# glmer(formula, data = , family = binomial)
# 1) formula:
# Abhängige Variable ~ Erklärende Variable + Random Factor
# In unseren Modellen kontrollieren wir für individuelle Unterschiede bei den Rehen
# indem wir einen Random Factor definieren => (1 | id)
# 2) data:
# euer Datensatz
# 3) family:
# hier binomial
# warum binomial? Verteilung Daten der abhängigen Variable Präsenz/Absenz
ggplot(DF_mod_day, aes(pres_abs)) +
geom_histogram()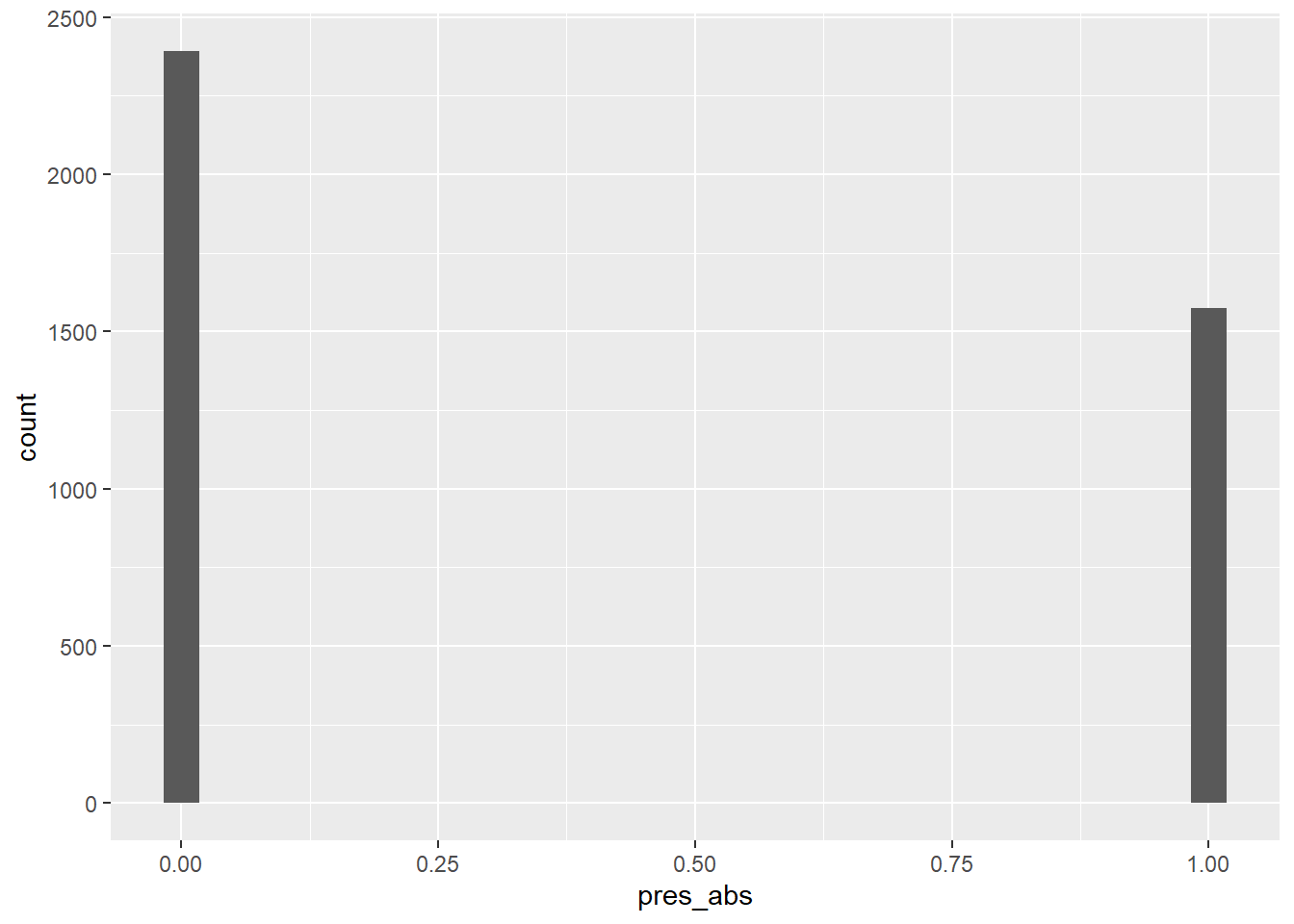
# --> Binäre Verteilung => Binomiale Verteilung mit n = 1
# und wie schaut die Verteilung der Daten der abhängigen Variable Nutzungsintensität
# (nmb, werden wir in diesem Kurs aber nicht genauer anschauen) aus?Aufgabe 4
Mit der GLMM Formel bauen wir in einem ersten Schritt eine univariate Variablenselektion auf.
Als abhängige Variable verwenden wir die Präsenz/Absenz der Rehe in den Kreisen
# Die erklärende Variable in m1 ist die erste Variable der korrelierenden Variablen
# Die erklärende Variable in m2 ist die zweite Variable der korrelierenden Variablen
modell_1 <- glmer(Abhaengige_Variable ~ Erklaerende_Variable + (1 | id),
data = DF_mod_day,
family = binomial
)
modell_2 <- glmer(Abhaengige_Variable ~ Erklaerende_Variable + (1 | id),
data = DF_mod_day,
family = binomial
)
# mit dieser Funktion können die Modellergebnisse inspiziert werden
summary(modell_1)
summary(modell_2)
# Mit dieser Funktion kann der Informationgehalt der beiden Modelle gegeneinander
# abgeschätzt werden
bbmle::AICtab(modell_1, modell_2)
# tieferer AIC -> besser (AIC = Akaike information criterion)
# ==> dieses Vorgehen muss nun für alle korrelierten Variablen für jeden Teildatensatz
# (Tag/Nacht) durchgeführt werden, um nur noch nicht (R < 0.7) korrelierte Variablen
# in das Modell einfliessen zu lassenMusterlösung
modell_1 <- glmer(pres_abs ~ dist_road_trails_scaled + (1 | id), data = DF_mod_day, family = binomial)
modell_2 <- glmer(pres_abs ~ dist_road_only_scaled + (1 | id), data = DF_mod_day, family = binomial)
summary(modell_1)
## Generalized linear mixed model fit by maximum likelihood (Laplace
## Approximation) [glmerMod]
## Family: binomial ( logit )
## Formula: pres_abs ~ dist_road_trails_scaled + (1 | id)
## Data: DF_mod_day
##
## AIC BIC logLik deviance df.resid
## 5104.9 5123.7 -2549.4 5098.9 3961
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -2.1046 -0.7564 -0.6277 1.0812 1.9219
##
## Random effects:
## Groups Name Variance Std.Dev.
## id (Intercept) 0.1996 0.4467
## Number of obs: 3964, groups: id, 12
##
## Fixed effects:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -0.31120 0.13418 -2.319 0.0204 *
## dist_road_trails_scaled 0.37745 0.03848 9.808 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Correlation of Fixed Effects:
## (Intr)
## dst_rd_trl_ -0.004
summary(modell_2)
## Generalized linear mixed model fit by maximum likelihood (Laplace
## Approximation) [glmerMod]
## Family: binomial ( logit )
## Formula: pres_abs ~ dist_road_only_scaled + (1 | id)
## Data: DF_mod_day
##
## AIC BIC logLik deviance df.resid
## 5098.4 5117.2 -2546.2 5092.4 3961
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -1.9625 -0.7615 -0.6080 1.0579 1.9425
##
## Random effects:
## Groups Name Variance Std.Dev.
## id (Intercept) 0.2103 0.4586
## Number of obs: 3964, groups: id, 12
##
## Fixed effects:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -0.3024 0.1375 -2.199 0.0279 *
## dist_road_only_scaled 0.3950 0.0389 10.154 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Correlation of Fixed Effects:
## (Intr)
## dst_rd_nly_ 0.002
bbmle::AICtab(modell_1, modell_2)
## dAIC df
## modell_2 0.0 3
## modell_1 6.5 3
# tieferer AIC -> besser (AIC = Akaike information criterion) -> als deltaAIC ausgewiesen
# Distanz zu Strassen (dist_road_only) = besser
modell_3 <- glmer(pres_abs ~ forest_prop_scaled + (1 | id), data = DF_mod_day, family = binomial)
modell_4 <- glmer(pres_abs ~ os_scaled + (1 | id), data = DF_mod_day, family = binomial)
summary(modell_3)
## Generalized linear mixed model fit by maximum likelihood (Laplace
## Approximation) [glmerMod]
## Family: binomial ( logit )
## Formula: pres_abs ~ forest_prop_scaled + (1 | id)
## Data: DF_mod_day
##
## AIC BIC logLik deviance df.resid
## 4726.1 4745.0 -2360.1 4720.1 3961
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -2.2952 -0.7853 -0.3909 0.9056 3.4113
##
## Random effects:
## Groups Name Variance Std.Dev.
## id (Intercept) 0.3069 0.554
## Number of obs: 3964, groups: id, 12
##
## Fixed effects:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -0.4351 0.1649 -2.639 0.00831 **
## forest_prop_scaled 0.8805 0.0443 19.878 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Correlation of Fixed Effects:
## (Intr)
## frst_prp_sc -0.060
summary(modell_4)
## Generalized linear mixed model fit by maximum likelihood (Laplace
## Approximation) [glmerMod]
## Family: binomial ( logit )
## Formula: pres_abs ~ os_scaled + (1 | id)
## Data: DF_mod_day
##
## AIC BIC logLik deviance df.resid
## 4863.0 4881.9 -2428.5 4857.0 3961
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -2.0044 -0.7984 -0.4421 0.9854 2.8754
##
## Random effects:
## Groups Name Variance Std.Dev.
## id (Intercept) 0.3228 0.5682
## Number of obs: 3964, groups: id, 12
##
## Fixed effects:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -0.34748 0.16847 -2.063 0.0392 *
## os_scaled 0.67559 0.03862 17.494 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Correlation of Fixed Effects:
## (Intr)
## os_scaled -0.029
bbmle::AICtab(modell_3, modell_4)
## dAIC df
## modell_3 0.0 3
## modell_4 136.9 3
# tieferer AIC -> besser (AIC = Akaike information criterion) -> als deltaAIC ausgewiesen
# Distanz zu Strassen (dist_road_only) = besserAufgabe 5
Selektion der Variablen in einem multivariaten Model
Mit folgendem Code kann eine automatisierte Variablenselektion (dredge-Funktion) und ein Modelaveraging aufgebaut werden (siehe auch Stats-Skript von J.Dengler & Team)
# hier wird die Formel für die dredge-Funktion vorbereitet (die Variablen V1-V6
# sind jene welche nach der univariaten Variablenselektion noch übrig bleiben)
f <- pres_abs ~
V1 +
V2 +
V3 +
V4 +
V5 +
V6
# in diesem Befehl kommt der Random-Factor (das Reh) hinzu und es wird eine Formel
# daraus gemacht
f_dredge <- paste(c(f, "+ (1 | id)"), collapse = " ") |> as.formula()
# Das Modell mit dieser Formel ausführen
m <- glmer(f_dredge, data = DF_mod_day, family = binomial, na.action = "na.fail")
# Das Modell in die dredge-Funktion einfügen (siehe auch unbedingt ?dredge)
all_m <- dredge(m)
all_m
# Importance values der einzelnen Variablen (Gibt an, wie bedeutsam eine bestimmte
# Variable ist, wenn man viele verschiedene Modelle vergleicht (multimodel inference))
sw(all_m)
# Schlussendlich wird ein Modelaverage durchgeführt (Schwellenwert für das delta-AIC = 2)
avgmodel <- model.avg(all_m, rank = "AICc", subset = delta < 2)
summary(avgmodel)
# ==> für den Nachtdatensatz muss der gleiche Prozess der Variablenselektion
# durchgespielt werden.Musterlösung
# hier wird die Formel für die dredge-Funktion vorbereitet (die Variablen V1-V6
# sind jene welche nach der univariaten Variablenselektion noch übrig bleiben)
f <- pres_abs ~
slope_scaled +
topo_pos_scaled +
us_scaled +
forest_prop_scaled +
dist_road_only_scaled +
dist_sett_scaled
# in diesem Befehl kommt der Random-Factor (das Reh) hinzu und es wird eine Formel
# daraus gemacht
f_dredge <- paste(c(f, "+ (1 | id)"), collapse = " ") |> as.formula()
# Das Modell mit dieser Formel ausführen
m <- glmer(f_dredge, data = DF_mod_day, family = binomial, na.action = "na.fail")
# Das Modell in die dredge-Funktion einfügen (siehe auch unbedingt ?dredge)
all_m <- dredge(m)
# Importance values der einzelnen Variablen (Gibt an, wie bedeutsam eine bestimmte
# Variable ist, wenn man viele verschiedene Modelle vergleicht (multimodel inference))
sw(all_m)
## dist_road_only_scaled forest_prop_scaled us_scaled
## Sum of weights: 1.00 1.00 1.00
## N containing models: 32 32 32
## slope_scaled dist_sett_scaled topo_pos_scaled
## Sum of weights: 0.99 0.46 0.30
## N containing models: 32 32 32
# Schlussendlich wird ein Modelaverage durchgeführt (Schwellenwert für das delta-AIC = 2)
avgmodel <- model.avg(all_m, rank = "AICc", subset = delta < 2)
summary(avgmodel)
##
## Call:
## model.avg(object = get.models(object = all_m, subset = delta <
## 2), rank = "AICc")
##
## Component model call:
## glmer(formula = pres_abs ~ <4 unique rhs>, data = DF_mod_day, family =
## binomial, na.action = na.fail)
##
## Component models:
## df logLik AICc delta weight
## 1346 6 -2268.17 4548.37 0.00 0.38
## 12346 7 -2267.34 4548.71 0.34 0.32
## 13456 7 -2268.01 4550.04 1.68 0.16
## 123456 8 -2267.16 4550.35 1.98 0.14
##
## Term codes:
## dist_road_only_scaled dist_sett_scaled forest_prop_scaled
## 1 2 3
## slope_scaled topo_pos_scaled us_scaled
## 4 5 6
##
## Model-averaged coefficients:
## (full average)
## Estimate Std. Error Adjusted SE z value Pr(>|z|)
## (Intercept) -0.432191 0.139554 0.139597 3.096 0.00196 **
## dist_road_only_scaled 0.416554 0.046861 0.046875 8.886 < 2e-16 ***
## forest_prop_scaled 0.818821 0.057266 0.057282 14.295 < 2e-16 ***
## slope_scaled -0.158651 0.049230 0.049245 3.222 0.00127 **
## us_scaled 0.390805 0.041070 0.041083 9.513 < 2e-16 ***
## dist_sett_scaled -0.036839 0.058045 0.058054 0.635 0.52571
## topo_pos_scaled 0.006678 0.022846 0.022852 0.292 0.77013
##
## (conditional average)
## Estimate Std. Error Adjusted SE z value Pr(>|z|)
## (Intercept) -0.43219 0.13955 0.13960 3.096 0.00196 **
## dist_road_only_scaled 0.41655 0.04686 0.04688 8.886 < 2e-16 ***
## forest_prop_scaled 0.81882 0.05727 0.05728 14.295 < 2e-16 ***
## slope_scaled -0.15865 0.04923 0.04924 3.222 0.00127 **
## us_scaled 0.39081 0.04107 0.04108 9.513 < 2e-16 ***
## dist_sett_scaled -0.08030 0.06208 0.06210 1.293 0.19597
## topo_pos_scaled 0.02197 0.03717 0.03718 0.591 0.55451
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Musterlösung
#| eval: false
#| error: true
#| echo: false
# hier wird die Formel für die dredge-Funktion vorbereitet (die Variablen V1-V8
# sind jene welche nach der univariaten Variablenselektion noch übrig bleiben)
f <- pres_abs ~
slope_scaled +
topo_pos_scaled +
us_scaled +
os_scaled +
forest_prop_scaled +
dist_road_only_scaled +
dist_road_trails_scaled +
dist_sett_scaled
# inn diesem Befehl kommt der Random-Factor (das Reh) hinzu und es wird eine Formel
# daraus gemacht
f_dredge <- paste(c(f, "+ (1 | id)"), collapse = " ") |> as.formula()
# Das Modell mit dieser Formel ausführen
m <- glmer(f_dredge, data = DF_mod_day, family = binomial, na.action = "na.fail")
car::vif(m)
## slope_scaled topo_pos_scaled us_scaled
## 1.514328 1.083853 1.242521
## os_scaled forest_prop_scaled dist_road_only_scaled
## 2.626511 2.664066 5.844383
## dist_road_trails_scaled dist_sett_scaled
## 5.674976 1.427576
mean(car::vif(m))
## [1] 2.759777